Взаимодействие быстрых электронов с веществом

1. Столкновение электронов с нейтральными атомами имеет, как правило, неупругий характер. Сталкиваясь с кристалличекой решёткой твёрдого тела или с атомами жидкости, электрон тормозится, сбрасывая энергию своего движения в виде тормозного электромагнитного излучения.

При скорости движения v до 1 км ç с излучаются электромагнитные волны метрового и сантиметрового диапазонов с l ³ 1 см. При скорости в пределах от 1 км ç с до 670 км ç с излучаются электромагнитные волны миллиметрового и ИК диапазонов.

Более высокие скорости движения (не тепловые) электроны получают, разгоняясь в электрических полях. Ускоряющее напряжение U сообщает электрону кинетическую энергию m_еv ² ç 2 = eU. Пройдя разность потенциалов 1 В, электрон приобретает скорость 480 км ç с и кинетическую энергию 1,6·10^-19 Дж = 1 эВ. В атомной и ядерной физике принято измерять энергию частиц в электрон-вольтах.

Если энергия электрона составляет от 1,4 до 124 эВ, то при торможении он испускает фотоны в видимом и УФ диапазонах. При дальнейшем нарастании энергии вплоть до 20 кэВ тормозящийся электрон испускает кванты ЭМ энергии в рентгеновском диапазоне.

Тормозное излучение имеет сплошной спектр. Коротковолновая граница спектра l _min определяется энергией электрона. еU =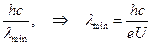. (9.1)

Электроны с энергией более 30 кэВ способны проникнуть внутрь электронной оболочки атома и выбить электроны с нижних уровней. После чего возбуждённый атом излучает узкие линии характеристических рентгеновских лучей, появляющиеся на фоне сплошного тормозного спектра.

Движение электронов со скоростью, большей фазовой скорости света в данном веществе (v > сçn) вызывает специфический эффект – свечение Вавилова-Черенкова.

Эти два явления – характеристические рентгеновские лучи и свечение Вавилова - Черенкова и рассматриваются в данном параграфе.

2. Рентгеновская спектроскопия. Для исследования рентгеновских спектров (спектров Х - лучей) нужен спектрометр – прибор, позволяющий не только регистрировать факт излучения в рентгеновском диапазоне, но и измерять длину волны l (частоту n) этого излучения. В основе рентгеновской спектрометрии лежит дифракция Х – лучей на кристаллах (см. Оптика, §34). Исторически были разработаны три практических метода.

а. Метод Лауэ, 1912г. Реализуется в проходящих лучах. Узкий пучок Х – лучей, выделяемый отверстием в свинцовом экране, проходит через монокристалл К, играющий роль пространственной дифракционной решетки (рис.55).

В методе Лауэ используются Х – лучи со сплошным тормозным спектром. Поэтому всегда находятся лучи тех длин волн, для которых выполняется условие главных максимумов в проходящих лучах. В результате на фотопластинке Фп, расположенной за кристаллом, образуется система точечных почернений.

На рис.56 показана фотография дифракционной картины Х – лучей на кристалле кварца, полученная по методу Лауэ (лауэграмма). По мере удаления от центра длина волны Х – лучей меняется. Поэтому в принципе лауэграммы можно использовать для определения длин волн l рентгеновского излучения. Однако расшифровка лауэграмм очень кропотливое и трудоемкое дело.

б. Метод Вульфа-Брэггов,1912г. Реализуется в отраженных лучах. Если на поверхность монокристалла направить пучок монохроматических Х – лучей, то при некоторых углах скольжения q будет выполняться условие главных максимумов в отраженных лучах (рис.57). 2 d sin q = kl. Формула Вульфа-Брэггов, 1912. (9.2)

Схема установки показана на рис.58. Пучок лучей из рентгеновской трубки падает под углом скольжения q на грань монокристалла K и отражается под тем же углом. Столик с кристаллом медленно поворачивается. Вокруг кристалла по дуге окружности расположена фотопластинка Фп. Когда угол q соответствует условию главного максимума (9.2), в отраженных Х – лучах возникает дифракционная вспышка, в результате на фотопленке в этом месте остается спектральная линия.

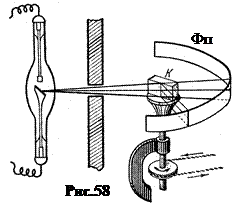Если пучок монохроматический, то спектральные линии имеют примерно одинаковую интенсивность и располагаются на фотопластинке в соответствии с формулой (9.2) симметрично оси падающего на кристалл луча.

Процесс исследования ускоряется, если вместо фотопластинки использовать ионизационную камеру, расположенную на отраженном луче и движущуюся по дуге с удвоенной угловой скоростью. (Дело в том, что при повороте зеркала-кристалла на угол a отраженный луч поворачивается на угол 2 a). В этом случае спектральным линиям соответствуют всплески электрического тока, пропорциональные интенсивности линий. Эти всплески регистрируются на самописце или в памяти ЭВМ.

Метод Вульфа - Брэггов лежит в основе большинства рентгеновских спектрометров, которые в принципиальной своей части повторяют схему рис.58.

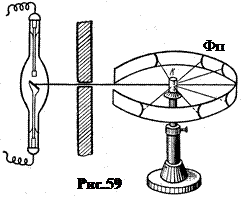
в. Метод Дебая - Шерера. В 1916г. немецкие физики Пауль Дебай и Петер Шерер предложили метод кристаллических порошков. Вместо качественного монокристалла, на котором осуществляется дифракция Х – лучей в первых двух методах, здесь используется спрессованный в цилиндрический столбик мелкокристаллический порошок (рис.59).

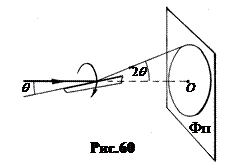
Если через такой столбик пропустить пучок монохроматических Х – лучей, то среди множества кристалликов в столбике всегда найдутся такие, которые расположены по отношению к лучу под углом, удовлетворяющим условию (9.2) для данной длины волны l. В результате возникает система лучей – конусов с углом при вершине 2 q, соответствующих дифракционным максимумам (рис.60).

Если окружить столбик фотопленкой, как показано на рис.59, то эти конусы оставляют на пленке следы в виде кривых линий, каждая из которых соответствует определенной длине волны l и порядковому номеру k максимума.

Огромное преимущество метода Дебая – Шерера состоит в простоте технологии приготовления образцов (прессование порошков или получение поликристаллических отливок). Поэтому он широко применяется в рентгеноструктурном анализе. Именно этот метод лежит в основе опытов Дж.П.Томсона по дифракции электронов. (См. §3 пункт 3 на с. 15).

3. Рентгеновские спектры. В первое десятилетие XX века было выполнено большое число работ по изучению рентгеновских спектров. Оказалось, что по сравнению с оптическими спектрами рентгеновские спектры элементов много проще. Если оптические спектры элементов имеют сотни и даже тысячи (железо, Fe) спектральных линий, то рентгеновские спектры имеют 1-3 группы (серии) по несколько единиц линий в каждой. Число серий увеличивается с ростом порядкового номера Z элемента в таблице Менделеева.

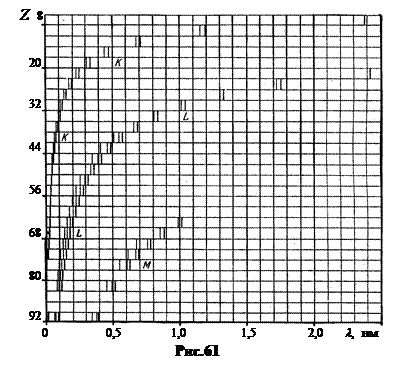На рис.61 показаны спектры характеристических рентгеновских лучей элементов с порядковыми номерами (сверху вниз) Z = 11, 14, 17, …92. По горизонтальной оси (вдоль спектров слева направо) отложена длина волны l от 0 до 2,5 нм.

Спектры легких элементов с Z от 11 (Na, натрий) до 22 (Ti, титан) имеют одну серию, спектры средних элементов с Z от 23 (V, ванадий) до 62 (Sm, самарий) имеют по 2 серии, спектры тяжелых элементов, начиная с редкоземельных (Z > 63) имеют по 3 серии и более.

Группы самых высокоэнергичных линий с наименьшими длинами волн l (на рис.61 крайние левые) стали обозначать буквой К (К - серия), следующие – буквами L (L - серия), М, N… Серии М и N имеются только у тяжелых элементов.

Из всех серий наиболее простую структуру имеет К – серия. Она состоит из трех линий К_a, К_b, К_g. Линия К_a самая длинноволновая и самая яркая. При высоком разрешении некоторые линии оказываются дублетами.

4. Закон Мозли. Уже при общем сравнении спектров на рис.61 становится ясно, что в расположении одноименных спектральных серий у разных элементов проявляется некоторая закономерность. Кривые, на которых располагаются серии, напоминают ветви параболы.

В 1914 г. Генри Мозли установил, что в отличие от оптических спектров многоэлектронных атомов, описывающихся формулой Ридберга (7.6) с поправками у квантовых чисел n и m, для рентгеновских спектров лучше подходит формула Бальмера с поправкой на атомный номер Z элемента 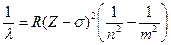. Закон Мозли, 1914. (9.2)

Здесь s - поправка (постоянная экранирования), мало отличающаяся от 1; n и m – главные квантовые числа, то есть номера энергетических уровней, соответствующих переходу электрона в атоме при испускании данной спектральной линии.

Открытая Мозли закономерность (закон Мозли) имеет принципиальное значение. Закон Мозли утверждает, что квадратный корень из обратной длины волны линии одноименной спектральной серии пропорционален порядковому номеру элемента Z.

Для головной линии К_a формула (9.2) принимает вид: 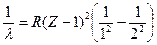. (9.3)

Для линии К_b m = 3, для линии К_g m = 4. К - серия напоминает серию Лаймана в спектре атома водорода. Излучение К - серии возникает при переходе электрона на первый, самый низкий энергетический уровень (n = 1) со 2-го (К_a), с 3-го (К_b), с 4-го (К_g) уровней.

Для L - серии закон Мозли имеет вид: 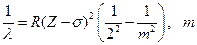= 3, 4, 5. (9.4)

Энергия квантов L - серии меньше, а длина волны l больше, чем соответствующих линий в К - серии. L - серия аналогична серии Бальмера в спектре атома водорода.

Для М - серии: 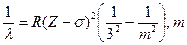=4,5,... (9.5)

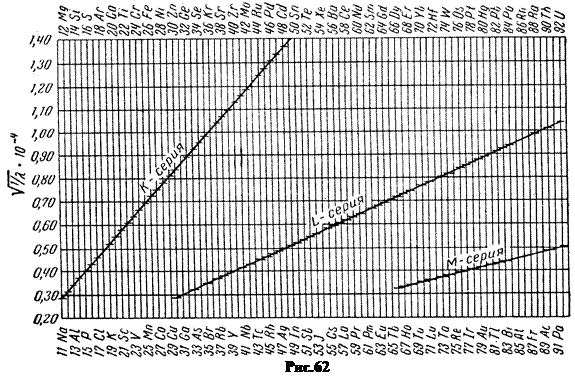На рис.62 показана диаграмма Мозли – график, где по вертикальной оси отложены значения 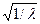, а по горизонтальной – порядковые номера Z элементов. Поражает точность выполнения закона Мозли. Точки каждой серии лежат строго на одной прямой.

С уменьшением номера Z элементов длина волны l ЭМ излучения увеличивается и постепенно выходит из рентгеновского в УФ и видимый диапазон. Граница между рентгеновским и УФ диапазонами условна. Если принять для верхней границы рентгеновского диапазона l = 10 нм, то из формулы (9.3) можно определить номер Z элемента, начиная с которого и ниже электронная оболочка атома не может излучать рентгеновские лучи. = 4. Водород, гелий, литий, бериллий в принципе не могут излучать рентгеновские лучи по причине малой энергии атомов в возбужденном состоянии. Реально доступная для измерений К - серия появляется у элементов, начиная с натрия, Z = 11. Другие серии появляются у еще более тяжелых элементов.

5. Механизм возникновения рентгеновских спектров состоит в том, что свободный быстрый электрон, влетающий в атом, выбивает из атома его собственный электрон с низкого энергетического уровня. Если “свой” электрон выбит с К - слоя, то в К - слое образуется вакансия. Какой-либо выше расположенный электрон атома, занимая вакансию, излучает квант К - серии. Если электрон выбивается с L - слоя, получается L - серия и т.д.

Характеристические рентгеновские лучи, выходя из глубин атома, несут информацию о внутреннем строении атома. Исторически закон Мозли сыграл большую роль в уточнении таблицы Менделеева, в частности, в распределении редкоземельных элементов.

Практическое значение рентгеновских спектров в том, что они представляют собой надежное средство химического анализа веществ. В отличие от оптических спектров, генерируемых внешней оболочкой атома и меняющихся при вступлении атома в разные химические соединения, рентгеновские спектры практически не зависят от межатомных связей. Рентгеновский спектр сложного вещества есть сумма спектров составляющих его элементов.

6. Излучение Черенкова. В начале 20 века работавшая с радиоактивными материалами Мария Кюри наблюдала слабое свечение растворов солей радия. Она истолковала это свечение как люминесценцию раствора под действием радиоизлучения. (Подобно вспышкам сернистого цинка ZnS под действием a - частиц в спинтарископе Крукса.)

В 1934 году Павел Черенков, работавший под руководством Сергея Вавилова над проблемой свечения растворов под действием g - излучения радия, установил, что растворы действительно люминесцируют. Но наряду с люминесценцией растворов существует еще дополнительное излучение, которое под действием g -лучей возникает и в чистых растворителях – воде H₂O, бензоле C₆H₆ и др. Глубокое исследование этого явления показало, что свечение чистых растворов вызывается не самими g -лучами, а быстрыми электронами, выбитыми g - квантами из атомов вещества. Излучение имеет определенное направление в пространстве, связанное с направлением движения электронов. Тогда как люминесценция излучается по всем направлениям равномерно.

В 1937 году Илья Франк и Игорь Тамм разработали строгую теорию излучения Черенкова. В соответствии с этой теорией, подтвержденной опытом, излучение возникает в результате интенсивной локальной поляризации вещества диэлектрических жидкостей, обусловленной быстрыми электронами, скорость которых v больше фазовой скорости света в этом веществе, v > сçn. Здесь n - показатель преломления жидкости.

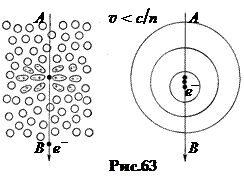7. Природа излучения Черенкова. Когда электрон движется в диэлектрической жидкости, оказавшиеся вблизи от него молекулы поляризуются (рис.63, слева). Буквой e на рисунке обозначен электрон, АВ – направление его движения. При медленном движении электрона поляризация молекул имеет не только осевую симметрию относительно траектории его движения, но одинакова спереди и сзади. В результате смещения поляризационных зарядов возникает электромагнитный импульс. Направленный в начале в одну сторону, а при исчезновении поляризации после прохождения электрона – в другую. Хотя эти импульсы не совпадают по времени, суммарный импульс на большом расстоянии от электрона оказывается довольно слабым.

Поскольку электрон движется медленно, то возбуждаемые поляризацией волны не образуют единого волнового фронта (рис.63 справа). В результате излучение получается очень слабым, равномерным по всем направлениям.

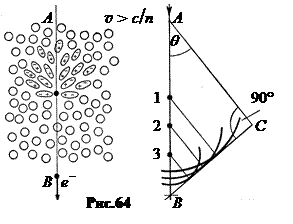
Ситуация существенно меняется, когда скорость электрона больше фазовой скорости света в веществе. В этом случае релаксация молекул происходит уже после ухода электрона. Симметрия поляризации спереди - сзади нарушается (рис.64, слева). Импульс электромагнитного излучения усиливается. (Качественно это видно хотя бы из того, что сопротивление движению электрона из-за несимметричной поляризации увеличивается.) А благодаря тому, что скорость электрона больше фазовой скорости света, v > сçn, у поляризационного излучения возникает единый волновой фронт ВС, направленный под углом q к вектору скорости v движения электрона (рис.64 справа).

Если путь АВ электрон проходит за время t, АВ = vt, то за это же время свет с фазовой скоростью сçn пройдет расстояние АС = (сçn)· t. Если среда изотропна (не кристалл), то угол между лучом АС и фронтом ВС прямой.Поэтому cos q =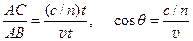. (9.6)

Излучение Черенкова формируется в узком коническом слое с углом при вершине 2 q. За счет этой направленности возникает усиление интенсивности излучения.

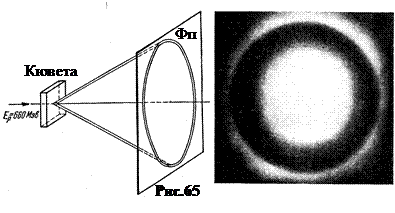На рис.65 слева показана схема опыта Черенкова, поставленного им в Дубне в 1959 году. В качестве источника быстрых заряженных частиц использовался протонный ускоритель с энергией протонов 660 МэВ. На оси конуса излучения ставилась фотопластинка Фп. На полученной фотографии (рис.65 справа) центральное светлое пятно образовано прямым пучком протонов, прошедших сквозь жидкость. Излучение Черенкова образовало кольцо.

Поскольку угол 2 q при вершине светового конуса зависит от скорости заряженных частиц, то на основе излучения Черенкова построены черенковские счетчики, позволяющие регистрировать быстрые заряженные частицы и определять их энергию.