2014-02-02
957
КОНСПЕКТ ЛЕКЦИЙ
Кафедра информатики и методики преподавания математики
Комплект учебно-методических материалов к учебной дисциплине:
Для направления 080800 Прикладная информатика
Профиль Прикладная математика в образовании
Ведущий лектор:
Вахитов Р.Х, доцент, кандидат физико-математических наук, доцент
Воронеж
Тема: Элементы теории множеств
Основные вопросы, рассматриваемые на лекции:
1. Конечные множества.
3. Диаграммы Эйлера – Венна.
4. Отношения между множествами.
5. Теорема о числе подмножеств конечного множества.
Краткое содержание лекционного материала
1. Конечные множества. Множество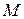 
называется конечным, если оно пустое или может быть задано перечислением элементов в виде конечной последовательности: 
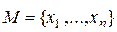. Множество, заданное перечислением элементов, не зависит от того, повторяются элементы или нет, и не зависит от того, переставляются элементы или нет. Например, 
, 
.
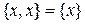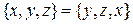Множество 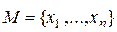называется 
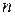-множеством, если все элементы 
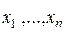попарно различны. Число 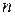при этом называется числом элементов (или мощностью) множества 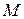и обозначается 
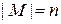. Число элементов пустого множества равно нулю: 
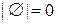. Если множество не конечное, то оно называется бесконечным. Понятие мощности множества обобщается и на бесконечные множества. Мощности бесконечных множеств могут быть различными, например, множества 
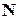и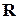 
имеют различные мощности.
2. Операции над множествами. Перечислим известные четыре бинарные операции и одну унарную операцию над множествами.
Объединением двух множеств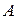 
и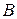 
называется множество всех элементов, принадлежащих хотя бы одному из множеств 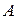и :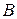
.
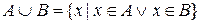Пересечением двух множеств 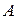и 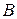называется множество всех элементов, принадлежащих одновременно каждому из множеств 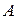и :
.
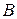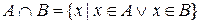Разностью множеств 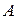и 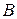называется множество всех элементов, принадлежащих множеству 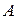, но не принадлежащих множеству :
.
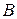Симметрической разностью множеств 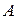и 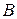называется объединение двух разносте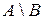й 
и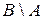 
:
.
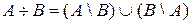Универсальное множество – это множество всех исследуемых объектов.
Дополнением множества 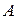называется разность универсального множества 
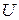и множества :
.
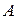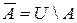3. Диаграммы Эйлера – Венна. Свойства отношений между множествами и операций над множествами можно наглядно проиллюстрировать с помощью диаграмм Венна (или кругов Эйлера). Каждое данное множество изображается в виде круга. Универсальное множество изображается в виде прямоугольника.
Результаты операций выделяются в виде частей круга и их соединений.
4. Отношения между множествами. Перечислим известные четыре бинарных отношения между множествами.
Два множества 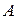и 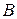называются равными 
, если
.
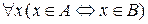Множество 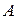называется подмножеством множества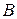 
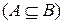, если
.
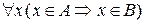Множество 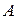называется собственным подмножеством множества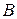 
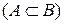, есл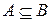и 
и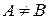 
.
Говорят, что множества 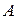и 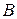не пересекаются, если 
.
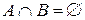5. Теорема о числе подмножеств конечного множества. Существует множество, содержащее все подмножества данного множества 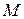. Оно называется множеством всех подмножеств множества 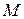и обозначается 
:
.
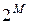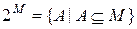Примеры. Если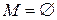 
, то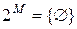 
. Если 
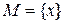, то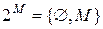 
.
Теорема 1. Пусть множество 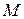конечно. Тогда 
.
Доказательство. Применим математическую индукцию по числу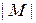 
элементов множества 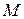. Заметим, что 
.
База индукции: 
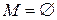. Тогда , и 
.
Шаг индукции: допустим, что 
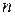, и для всех множеств с элементами утверждение теоремы 1 выполнено. Так как 
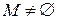, можно выбрать некоторый элемент 
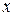множества 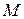. Поскольку 
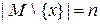, то по индуктивному предположению множество 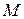имеет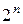 
подмножеств, не содержащих элемента 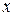. Столько же у него подмножеств, содержащих элемент 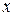. Следовательно, 
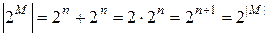. Теорема 1 доказана.
