Тема: эйлеровы графы
Основные вопросы, рассматриваемые на лекции:
1. Маршруты, цепи и циклы
2. Задача о кенигсбергских мостах. Эйлеровы графы
3. Задача о кругосветном путешествии. Гамильтоновы графы
4. Примеры (не)эйлеровых и (не)гамильтоновых графов
Краткое содержание лекционного материала
1. Маршруты, цепи и циклы. Маршрут (или путь) в графе – это чередующаяся последовательность вершин и ребер u 1, p 1, u 2, p 2, …, un, pn, un +1, начинающаяся и кончающаяся вершиной, и каждое ребро pi инцидентно вершинам ui и ui +1, где i =1,…, n.
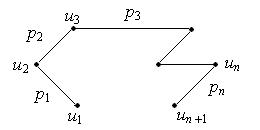
Этот маршрут обычно обозначается по вершинам: u 1 u 2… unun +1.
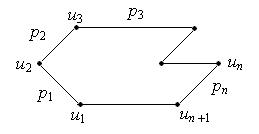
Маршрут называется замкнутым, если un +1= u 1, и открытым, если un +1¹ u 1.
Цепь – это открытый маршрут, в котором все ребра различны.
Простая цепь – это маршрут, в котором все вершины различны.
Если в маршруте два ребра равны, то равны и вершины – их концы. Значит, если все вершины маршрута различны, то и все ребра различны, поэтому простая цепь является цепью.
Пример 1. Рассмотрим граф с вершинами 1, 2, 3, 4, 5 и 6 с ребрами {1,2}, {1,4}, {2,3}, {2,4}, {2,5}, {3,5}, {3,6} и {5,6}.
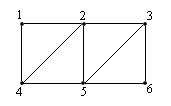
Приведем некоторые открытые маршруты в этом графе.
Маршрут 1253256 не является цепью.
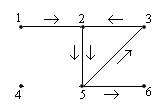
Маршрут 1245236 является цепью, но не является простой цепью.
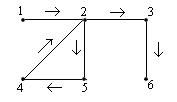
Маршрут 124536 является простой цепью.

Цикл – это замкнутая цепь. Простой цикл – это замкнутая простая цепь с числом вершин ³3.
Приведем некоторые замкнутые маршруты в графе примера 1.
Маршрут 12532541 не является циклом.
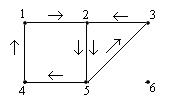
Маршрут 1235241 является циклом, но не является простым циклом.
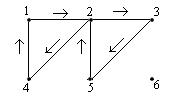
Маршрут 1235241 является простым циклом.

2. Задача о кенигсбергских мостах. Эйлеровы графы. В 1736г. Леонард Эйлер решил задачу о кёнигсбергских мостах.
Четыре части суши – два берега (точки A и D) и два острова (точки B и C) соединены семью мостами:
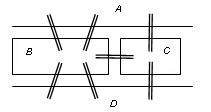
Надо прогуляться по замкнутому маршруту, так, чтобы пройти через каждый из мостов только один раз.
Решение задачи сводится к рассмотрению следующего мультиграфа и к поиску в нем замкнутого маршрута, проходящего через все ребра ровно по одному разу:

Эйлеров цикл в мультиграфе – это цикл, содержащий все ребра.
Граф называется эйлеровым, если содержит эйлеров цикл.
Пример эйлерова графа:
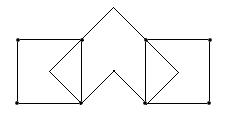
Граф называется связным, если любые его две вершины соединены некоторой цепью.
Теорема 1. Граф G эйлеров тогда и только тогда, когда граф G связный граф и степень каждой вершины графа G есть чётное число.
Доказательство. Если граф G эйлеров, т.е. содержит цикл, проходящий через все ребра графа G, то, значит, граф связный, а каждая вершина графа инцидентна четному числу ребер: вместе с каждым ребром – «входом» цикла в вершину должно быть ребро – «выход» цикла из вершины.
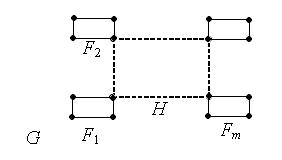
Обратно, индукцией по числу ребер доказываем, что если граф G связный, а каждая вершина графа инцидентна четному числу ребер, то в графе найдется подграф – эйлеров цикл. Поскольку граф связный и степени вершин – четные числа, то степень каждой вершины не меньше 2, значит, в графе G найдется хотя бы один цикл H. Разность G / H распадается на связные компоненты, содержащие тоже вершины с четными степенями, значит, по индуктивному предположению, содержащие эйлеровы циклы F 1, …, Fm. Соединяя подходящим образом граф H с графами F 1, …, Fm, получим эйлеров цикл в графе G.
3. Задача о кругосветном путешествии. Гамильтоновы графы. Задача Гамильтона: совершить кругосветное путешествие по ребрам додекаэдра, вершины которого символизировали крупные города Земли, при этом побывать в каждом городе ровно по одному разу.
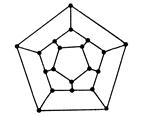
На рисунке – развертка додекаэдра.
Гамильтонов цикл – это простой цикл, проходящий через все вершины графа.
Гамильтонов граф – это граф, в котором содержащий хотя бы один гамильтонов цикл.
Полные графы – гамильтоновы.
Некоторые достаточные условия гамильтонова графа:
1) если степень каждой вершины 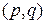 -графа
-графа 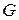 не меньше
не меньше 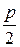 , то граф
, то граф 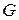 является гамильтоновым (условие Дирака);
является гамильтоновым (условие Дирака);
2) если сумма степеней любой пары несмежных вершин 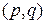 -графа
-графа 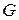 не меньше
не меньше 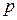 , то граф
, то граф 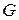 является гамильтоновым (условие Оре);
является гамильтоновым (условие Оре);
3) если для любого числа 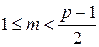 число вершин
число вершин 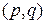 -графа
-графа 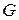 ,
, 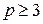 , со степенями не больших
, со степенями не больших 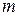 , меньше чем
, меньше чем 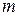 , и для нечетного
, и для нечетного 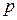 число вершин степени
число вершин степени 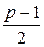 не больше
не больше 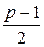 , то то граф
, то то граф 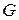 является гамильтоновым (условие Поша).
является гамильтоновым (условие Поша).
Условие Поша обобщает условия Дирака и Оре.
Связный граф называется 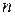 - связным, если для превращения его в несвязного графа нужно удалить не менее
- связным, если для превращения его в несвязного графа нужно удалить не менее 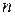 вершин.
вершин.
Пример трехсвязного графа – колесо 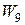 :
:
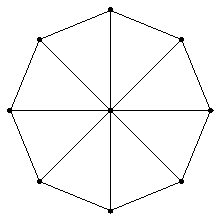
Связностью графа называется наименьшее число его вершин, удаление которых приводит к несвязному или тривиальному графу.
Легко видеть, что односвязные графы негамильтоновы.
Значит, гамильтоновы графы двусвязные, т.е. они связности 2 и более.
Тэта-графом называют граф, содержащий две вершины степени 3, соединенные тремя простыми попарно непересекающимися цепями длины не менее двух:
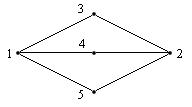
Если двусвязный граф содержит тета-граф, то он негамильтонов граф.
4. Примеры (не)эйлеровых и (не)гамильтоновых графов.
Приведем примеры графов, обладающих или не обладающих свойствами эйлеровости и гамильтоновости.
| граф | гамильтонов | Не гамильтонов |
| эйлеров | 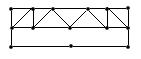 | 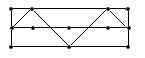 |
| не эйлеров | 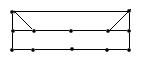 | 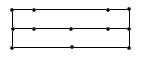 |
 2014-02-02
2014-02-02 4780
4780








