Лекция № 12.. Тема: плоские и планарные графы

Тема: плоские и планарные графы

Основные вопросы, рассматриваемые на лекции:

1. Двудольные графы

2. Плоские графы и плоские карты

3. Непланарность графов К_3,3 и К₅

Краткое содержание лекционного материала

1. Двудольные графы. Граф 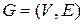называется двудольным 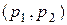- графом, если множество вершин 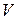состоит из двух непустых частей 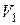, 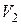(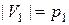, 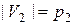), внутри которых нет ребер.

Если при этом все вершин из 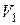соединены со всеми вершинами из 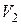, то граф 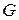называется полным двудольным 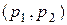- графом и обозначается через .

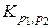Приведем полные двудольные графы с числом вершин не больше 4:

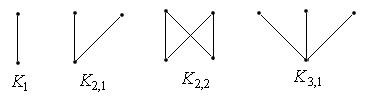
2. Плоские графы и плоские карты. Плоский граф – это граф, который нарисован на плоскости так, что никакие два его ребра не пересекаются.

Планарный граф – это граф, изоморфный плоскому графу.

На рисунке а) – планарный, но не плоский, граф, б) плоский граф.

Каждый плоский граф разбивает плоскость на грани: внутренние - ограниченные и внешнюю – неограниченную.

Изучение планарных графов было начато Эйлером в его исследованиях полиэдров. Следующая формула Эйлера – это классический результат в математике:

,

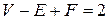где 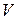– число вершин, 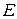– число ребер, 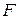– число граней полиэдра.

Формула Эйлера справедлива и в более общем случае для плоской карты – связного плоского графа, рассматриваемого вместе со всеми его гранями.

Теорема 1. Пусть плоская карта имеет 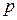вершин, 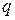ребер и 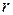граней. Тогда имеет место следующее равенство:

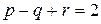. (1)

Доказательство. Применим индукцию по числу ребер .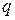

Если 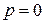, то формула (1) примет следующий вид: .

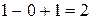Допустим, что для всех плоских карт с числом ребер не больше 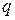формула (1) верна. Плоская карта с числом ребер 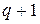получается из плоской карты с числом ребер 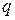двумя способами:

1) прибавлением новой вершины 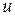, которая соединяется ребром 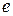с одной из старых вершин;

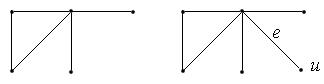
2) соединением ребром 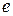двух не смежных вершин.

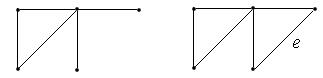
В первом случае формула (1) проверяется следующим образом:

.

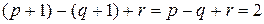Во втором случае появляется новая грань и формула (1) проверяется следующим образом:

.

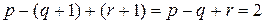Следствие 1. Если в 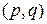-карте каждая грань образована циклом из 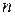вершин, то

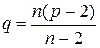. (2)

Доказательство. Число ребер, принадлежащих каждой грани равно 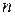. Значит, число вершин, подсчитываемых при каждой грани, равно 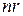. При этом каждое ребро подсчитывается дважды, поэтому число пересчитываемых вершин равно 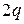. Получим равенство 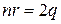. Подставим в (1) и найдем (2).