Максимальным планарным графом называется планарный граф, который при добавлении любого ребра перестает быть планарным.
Из определения следует, что в максимально планарном графе все грани являются треугольниками (гранями с тремя вершинами):
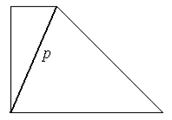
если грань содержит четырехугольник (или многоугольник с большим числом сторон), то можно добавить ребро 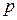 , не меняющее планарность графа, но лишающее свойства графа быть максимально планарным графом.
, не меняющее планарность графа, но лишающее свойства графа быть максимально планарным графом.
Пример 1. В следующий граф можно добавить только одно ребро, после которого этот граф обращается в граф 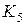 .
.
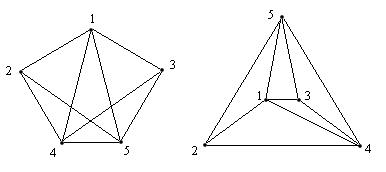
Максимальным планарным двудольным графом называется планарный двудольный граф, который при добавлении любого ребра перестает быть планарнымдвудольным графом.
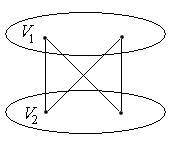
Если  – максимальный планарный двудольный граф, то каждая ее грань является четырехугольником:
– максимальный планарный двудольный граф, то каждая ее грань является четырехугольником:
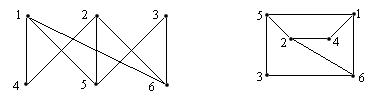
Пример 2. В следующий граф можно добавить только одно ребро, после которого этот граф обращается в граф 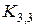 :
:
Следствие 2. Если 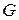 – планарный
– планарный 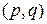 -граф и
-граф и 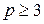 , то
, то
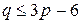 .
.
Доказательство. Наибольшим числом ребер в плоском графе обладает граф, у которого все грани – треугольники. В максимальном планарном графе все грани – треугольники. Подставим в (2) 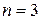 . Получим
. Получим 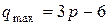 .
.
Следствие 3. Если 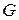 – планарный двудольный граф, то
– планарный двудольный граф, то 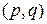 -граф, то
-граф, то
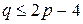 .
.
Доказательство. Наибольшим числом ребер в плоском двудольном графе обладает граф, у которого все грани – четырехугольники. В максимальном планарном графе все грани – четырехугольники. Подставим в (2) 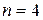 . Получим
. Получим 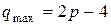 .
.
Теорема 2. Графы 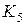 и
и 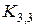 не планарные.
не планарные.
Доказательство. Если (5,10)-граф 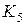 планарный, то не выполняется следствие 2:
планарный, то не выполняется следствие 2: 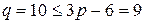 .
.
Если (6,9)-граф 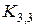 планарный, то не выполняется следствие 3:
планарный, то не выполняется следствие 3: 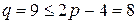 .
.
Теорема Куратовского. Граф планарен тогда и только тогда, когда не содержит подграфа, гомеоморфного 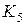 или
или 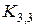 .
.
 2014-02-02
2014-02-02 5669
5669








