Тема: кратчайшие пути. Алгоритм Дейкстры
Основные вопросы, рассматриваемые на лекции:
1. Задача о кратчайшем пути на графе.
2. Определение алгоритма Дейкстры.
3. Выполнение алгоритма Дейкстры на примере графа.
Краткое содержание лекционного материала
1. Задача о кратчайшем пути на графе. Припишем всем ребрам графа веса – положительные числа. Кратчайший путь от вершины 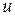 до вершины
до вершины 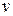 – это маршрут от
– это маршрут от 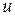 до
до 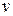 с минимальной суммой весов ребер маршрута. Надо найти все кратчайшие пути от данной вершины до всех остальных вершин.
с минимальной суммой весов ребер маршрута. Надо найти все кратчайшие пути от данной вершины до всех остальных вершин.
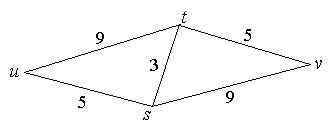
Пример. Маршрут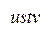 имеет сумму весов ребер 13, а маршруты
имеет сумму весов ребер 13, а маршруты 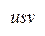 и
и 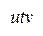 – 14. Значит,
– 14. Значит, 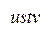 – кратчайший путь от
– кратчайший путь от 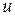 до
до 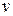 .
.
Задача о кратчайшем пути на графе решается алгоритмом, изобретенным нидерландским ученым Э. Дейкстрой в 1959 г.
Расстоянием от 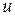 до
до 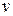 называют сумму весов ребер по одному из маршрута от
называют сумму весов ребер по одному из маршрута от 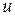 до
до 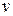 .
.
2. Определение алгоритма Дейкстры. Каждой вершине 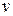 ставим метку – минимальное известное расстояние от данной вершины
ставим метку – минимальное известное расстояние от данной вершины 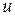 .
.
Алгоритм работает пошагово – на каждом шаге он «посещает» одну вершину и пытается уменьшить метку вершины. Если все вершины посещены, алгоритм завершается.
Метка вершины 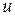 равна 0. В начале метки остальных вершин предполагаются равными +¥. Иначе, из ещё не посещённых вершин выбирается вершина
равна 0. В начале метки остальных вершин предполагаются равными +¥. Иначе, из ещё не посещённых вершин выбирается вершина 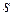 , имеющая минимальную метку. Рассматривают всевозможные маршруты с началом
, имеющая минимальную метку. Рассматривают всевозможные маршруты с началом 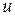 , в которых
, в которых 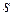 является предпоследним пунктом.
является предпоследним пунктом.
Для каждой не посещённой вершины 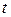 , смежной с вершиной
, смежной с вершиной 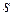 , находят сумму значения текущей метки
, находят сумму значения текущей метки 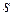 и веса ребра, соединяющего
и веса ребра, соединяющего 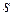 и
и 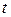 . Если полученная сумма s меньше значения t метки
. Если полученная сумма s меньше значения t метки 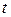 , то метку t заменяют меткой s.
, то метку t заменяют меткой s.
Рассмотрев все не посещённые вершины, смежные с вершиной 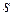 , вершина
, вершина  отмечается как посещенная, и повторяется шаг алгоритма.
отмечается как посещенная, и повторяется шаг алгоритма.
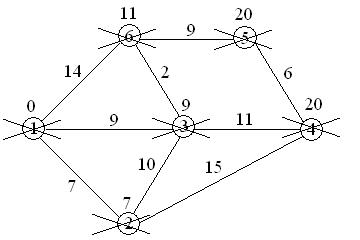
4. Выполнение алгоритма Дейкстры на примере графа. Требуется найти кратчайшие расстояния от 1-й вершины до всех остальных.
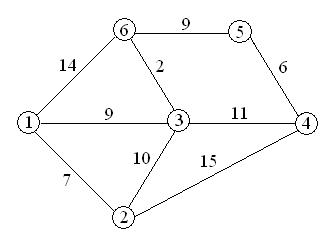
Кружками обозначены вершины, линиями – ребра графа. В кружках обозначены номера вершин, над ребрами обозначена их вес – (или длина пути).
Рядом с каждой вершиной обозначена метка – длина кратчайшего пути в эту вершину из вершины 1.
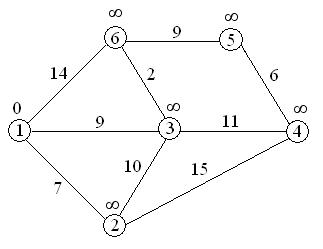
Первый шаг. Рассмотрим шаг алгоритма Дейкстры для нашего примера. Минимальную метку имеет вершина 1. Её соседями являются вершины 2, 3 и 6.
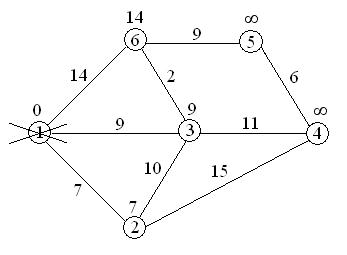
7<¥, поэтому метка ¥ при вершине 2 заменяется меткой 7,
9<¥, поэтому метка ¥ при вершине 3 заменяется меткой 9,
14<¥, поэтому метка ¥ при вершине 6 заменяется меткой 14,
вершина 1 вычеркивается из числа посещенных вершин.
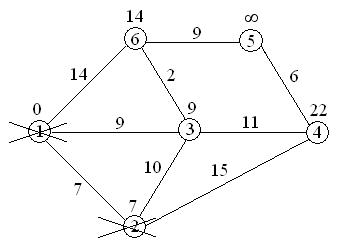
7+10=17>9, поэтому метка 9 при вершине 3 остается;
7+15=22<¥, поэтому метка ¥ при вершине 4 заменяется меткой 22;
вершина 2 вычеркивается из числа посещенных вершин.
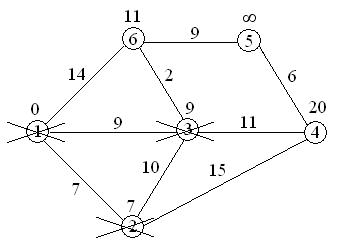
9+11=20<22, поэтому метка 22 при вершине 4 заменяется меткой 20;
9+2=11<14, поэтому метка 14 при вершине 6 заменяется меткой 11;
вершина 3 вычеркивается из числа посещенных вершин.
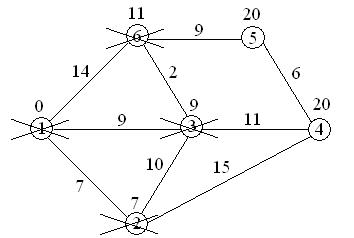
11+9=20<¥, поэтому метка ¥ при вершине 5 заменяется меткой 20;
вершина 6 вычеркивается из числа посещенных вершин.
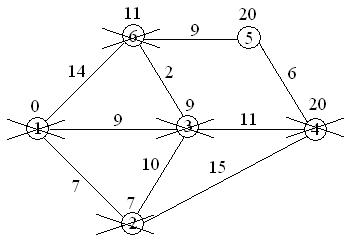
20+6=26>20, поэтому метка 20 при вершине 5 остается;
вершина 4 вычеркивается из числа посещенных вершин.
У вершины 5 не посещенных смежных вершин нет, поэтому вершина 5 также вычеркивается из числа не посещенных вершин.
Алгоритм заканчивает работу, так как нельзя больше обработать ни одной вершины. Кратчайшие пути – это последние метки при вершинах.
 2014-02-02
2014-02-02 2094
2094
