Основы теории напряженного и деформированного состояния
Контрольные вопросы
1. Когда брус испытывает деформацию центрального растяжения, сжатия?
2. Какие внутренние усилия возникают при ц.р.с.?
3. Какие напряжения возникают при ц.р.с.? Как они определяются?
4. Что такое абсолютная деформация? Относительная деформация?
5. Как сформулировать закон Гука в деформациях? Закон Гука в напряжениях?
6. Как сформулировать закон Пуассона?
7. Что такое предел пропорциональности? Предел упругости? Предел текучести (физический)? Предел текучести условный? Предел прочности?
8. Условие прочности при ц.р.с.?
9. Как определяется жёсткость при ц.р.с.?
10. Что называется допускаемым напряжением и как оно определяется?
11. Какие системы называются статически неопределимыми?
12. Какие уравнения используются при раскрытии статической неопределимости?
На различно ориентированных площадках, проходящих через одну и ту же точку, будут отличаться и по величине и по направлению.
Совокупность напряжений по всем площадкам, проходящим через данную точку, называется.напряженным состоянием в точке тела
 |
|
|
|
|

|
 |
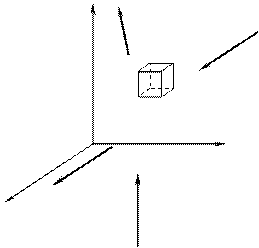
Так как все грани параллелепипеда бесконечно малы и в пределе проходят через точку А, то напряжения на соответствующих секущих плоскостях – это напряжения в исследуемой точке. Такой подход возможен на основании гипотезы сплошной среды.
|
|

Обозначим полные напряжения, действующие на гранях параллелепипеда Px, Py, Pz (рис. 4.1). Здесь индексы показывают нормаль к площадке, на которой действует напряжение. Эти полные напряжения раскладываются на три составляющие в направлении координатных осей: одно по нормали к площадке и два в ее плоскости (рис. 4. 2).
|
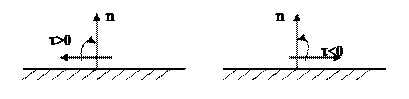
Согласно методу сечения, выделенный элемент под действием рассматриваемых напряжений будет находиться в равновесии. Вследствие достаточно малой длины ребер элемента напряжения на параллельных гранях можно считать равными, но противоположно
направленными. Поэтому напряженное состояние в точке может быть задано девятью компонентами по трем взаимно перпендикулярным площадкам
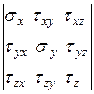
 2014-02-02
2014-02-02 874
874








