Молекулы жидкости, находящиеся на свободной поверхности (границе раздела «жидкость – газ» или «жидкость – пар»), в отличие от молекул, находящихся в срединных слоях, испытывают одностороннее воздействие со стороны соседних молекул. Поэтому на криволинейной поверхности должны возникать растягивающие усилия. Для количественного описания этого явления Юнгом была проведена классическая аналогия с упругой плёнкой. Натяжение этой плёнки характеризуется коэффициентом поверхностного натяжения [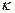 ]=Н/м. Величина
]=Н/м. Величина 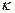 зависит, прежде всего, от природы контактирующих сред. Сила поверхностного натяжения всешда стремится сократить площадь свободной поверхности.
зависит, прежде всего, от природы контактирующих сред. Сила поверхностного натяжения всешда стремится сократить площадь свободной поверхности.
Коэффициент поверхностного натяжения 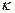 падает с ростом температуры и практически не зависит от давления. Поверхностное натяжение может быть существенно снижено с помощью поверхностно-активных веществ (ПАВ), к числу которых относятся моющие средства.
падает с ростом температуры и практически не зависит от давления. Поверхностное натяжение может быть существенно снижено с помощью поверхностно-активных веществ (ПАВ), к числу которых относятся моющие средства.
Величина 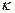 может служить мерой свободной энергии, которой обладает граница раздела:
может служить мерой свободной энергии, которой обладает граница раздела:
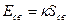 ,
,
где 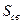 – площадь свободной поверхности. В этом случае
– площадь свободной поверхности. В этом случае 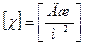 , что согласуется с ранее указанной размерностью.
, что согласуется с ранее указанной размерностью.
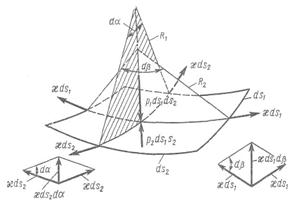
Равнодействующие сил поверхностного натяжения, действующие на границы выделенного контура, равны 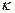 ds1 и
ds1 и 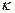 ds2 (рис. 1.2),а возникающая вследствие этого сила, действующая по нормалям к выделенной площадке, в первом приближении равна
ds2 (рис. 1.2),а возникающая вследствие этого сила, действующая по нормалям к выделенной площадке, в первом приближении равна 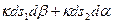 . С учетом того, что
. С учетом того, что 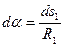 и
и 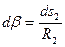 имеем выражение для силы:
имеем выражение для силы:
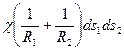 .
.
Эта величина, очевидно, и есть скачок давления на поверхности раздела двух сред, обусловленный поверхностным натяжением. Обозначив теперь через p1 и p2 и давления в средах на границе раздела из условия равновесия элементарной площадки, запишем соотношение
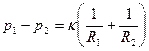 , (1.5)
, (1.5)
 |
которое называется формулой Лапласа.
Рис. 1.2 Криволинейная поверхность раздела.
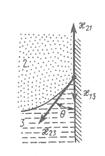 |
Рис. 1.3 Система «газ-жидкость-твёрдая стенка».
Для цилиндрических поверхностей с круговым поперечным сечением радиуса R имеем 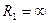 , R2=R и формула Лапласа приобретает такой вид:
, R2=R и формула Лапласа приобретает такой вид:
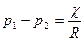
В случае сферических поверхностей R1=R2= R и тогда получаем:
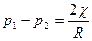
Весьма характерной является также система «газ - жидкость - твердая стенка» (рис. 1.3). В этом случае вводят значение краевого угла 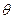 (угла контакта, или угла смачивания). Если
(угла контакта, или угла смачивания). Если 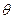 <
<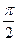 , жидкость называется смачивающей поверхность (данного твёрдого тела); если
, жидкость называется смачивающей поверхность (данного твёрдого тела); если 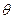 >
>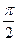 – несмачивающей.
– несмачивающей.
Введенное понятие краевого угла относится к статическому случаю. При движении линии раздела разных сред иногда вводят понятие динамического угла контакта, однако закономерности его поведения пока не выяснены.
 2014-02-02
2014-02-02 720
720








