Подобие и особенности моделирования течений капельных жидкостей

Тема 2. ТЕОРИЯ ПОДОБИЯ И МОДЕЛИРОВАНИЯ ТЕЧЕНИЙ ЖИДКОСТИ

(Лекций 2 ч., СРС 2 ч.)

Определение подобных течений. Два подхода к нахождению критериев подобия. Теория размерностей, p - теорема. Критерии подобия в течениях жидкости: числа Фруда, Рейнольдса, кавитации, Вебера и др.

Методы исследования задач механики жидкости: теоретические и экспериментальные. Техника и методика гидродинамических исследований.

Вопрос о подобии возникает в связи с необходимостью опытного, экспериментального определения важнейших характеристик течений капельных жидкостей. Если отбросить тепловые, электрические, электромагнитные и другие факторы, отличные от чисто механических, то систему «тело – жидкость» можно рассматривать как механическую. Тогда можно говорить о подобии механических систем, которые являются частным случаем более общих физических систем.

Два явления считаются подобными, если по известным характеристикам одного можно получить соответствующие характеристики другого простым пересчетом с использованием переходных масштабов. Иными словами, пересчет производится по правилам перехода от одной системы единиц величин к другой.

При сопоставлении механических систем различают три вида подобия.

Прежде всего, должно соблюдаться геометрическое подобие, которое означает, что отношение всех соответствующих длин геометрически подобных систем должно быть одинаковым.

Далее можно выполнить кинематическое подобие, согласно которому в любых сходственных точках скорости частиц параллельны и пропорциональны друг другу. Пусть 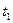- время, за которое частица проходит 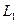в первой системе, а 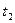- время, за которое частица проходит путь 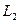во второй системе, l =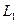/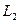и 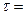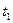/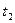. Тогда

/= /, /=/,

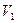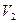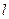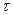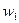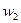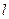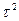где 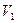,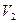- скорости, 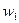,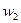- ускорения в первой и второй системах.

Механические системы с подобными распределениями масс должны удовлетворять условию

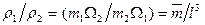
Где 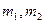- массы сходственных объемов в первой и второй системах,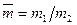

При существовании кинематического подобия такие системы будут динамически подобными.

Геометрическое подобие осуществляется просто путём изготовления уменьшенной в размерах копии натурного образца. Для обеспечения кинематического и динамического подобия нужно, прежде всего, обратиться к законам физики. В описании механических систем основную роль играет второй закон Ньютона. Запишем его для двух систем:

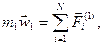
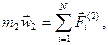
Здесь 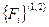- вектор сил, приложенных к материальным точкам сравниваемых систем. В кинематически и динамически подобных системах векторы ускорений центров тяжести должны быть одинаковы по направлению, а также должно быть равно число сил, приложенных к каждой системе, и в каждой из силы должны быть одинаково направлены. Из сказанного следует, что

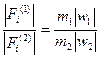(1.6)

Или

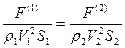(1.7)

Формула (1.7) представляет собой закон подобия Ньютона, утверждающий, что в динамически подобных системах должны быть равны безразмерные коэффициенты сил, которые образуются делением соответствующей силы на произведения соответствующих значений плотности, площади и квадрата скорости.

Закон подобия Ньютона позволяет записать безразмерные комплексы, отражающие действия сил той или иной природы. Эти комплексы называются критериями (или числами) подобия.

Пусть силы генерируются вязкостью. Согласно закону вязкого трения Ньютона

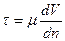
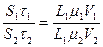
И на основании закона подобия (1.7) получаем

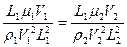
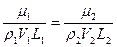
Таким образом, подобие течений по соотношению инерционных и вязких сил определяется безразмерным комплексом

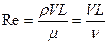, (1.8)

который называется числом Рейнольдса. Область применения: течения в трубах, обтекание вязкой жидкостью.

Рассмотрим теперь условия подобия для течений под действием сил тяжести, которые имеют объемный характер действия.

Условие подобия дает

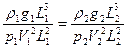
Или

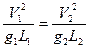
Безразмерный комплекс

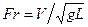
получил название числа Фруда (отношение инерционных сил к силам тяжести). Область применения: движение вблизи поверхностей раздела.

Отношение сил давления к инерционным силам приводит к понятию числа Эйлера. Область применения: течения сжимаемой среды.

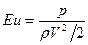
В течениях с естественной кавитацией обычно известно давление в невозмущенном потоке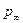и давление насыщенного пара в каверне 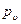. Если принять разность между этими давлениями как масштабный коэффициент, то можно ввести в рассмотрение модифицированное число Эйлера, которое обычно называют числом естественной (паровой) кавитации;

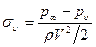(1.9)

В течениях с искусственной кавитацией вместо давления 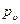нужно учитывать давление в каверне 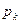, и тогда формула (1.9) дает определение числа искусственной кавитации

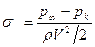
Для анализа распределения давления удобно пользоваться безразмерным коэффициентом давления

,

где р - давление в данной точке.

Если рассматривать теперь капельную жидкость как среду сжимаемую, то получим ещё один критерий подобия, характеризующий сжимаемость среды:

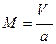, называемый числом Маха.

Если обратимся к силам, обусловленным поверхностным натяжением, то можно ввести понятие числа Вебера, представляющего собой отношение инерционных сил к силам поверхностного натяжения:

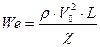
Область применения критерия Вебера: течения с поверхностным натяжением на свободных границах.

В силу того, что нагрузки при движении тела в воде велики, целесообразно рассмотреть случай, когда проявляется упругость тела, т.е. наблюдается явление гидроупругости.

Критерий Коши: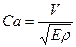

В нестационарных течениях рассматривается безразмерный комплекс:

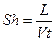
получил название числа Струхаля (отношение силы нестационарной среды к инерционной силе). Область применения: нестационарные течения.

Рассмотренные критерии подобия охватывают большинство практических задач гидромеханики. Вместе с тем встречаются и другие безразмерные параметры, отражающие своеобразие той или иной задач.

Теперь можно более развёрнуто сформулировать принцип динамического подобия потоков. В динамически подобных течениях капельных жидкостей в общем случае должны быть равными критерии подобия Re, Fr, We, Sh, M, Ca, Eu, σ.

Вид и число критериев подобия, рассматриваемых в конкретной задаче, большей частью устанавливается на основании анализа математической формулировки задачи.