Силы, действующие на жидкую частицу, подразделяются на два типа: объемные и поверхностные.
К объемным (или массовым) силам принадлежат, например, сила тяжести, центробежная сила. Массовые силы другой природы здесь не рассматриваются. Объемные силы действуют в каждой точке элементарного объема сплошной среды. Пусть 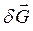 – главный вектор объемных сил, действующих в объеме
– главный вектор объемных сил, действующих в объеме 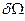 . Тогда вводится понятие плотности распределения объемных сил в виде предела:
. Тогда вводится понятие плотности распределения объемных сил в виде предела:
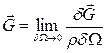 . ( 2.1 )
. ( 2.1 )
Как видим, размерность 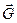 соответствует размерности ускорения:
соответствует размерности ускорения: 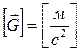 . Весу, например, соответствует равенство
. Весу, например, соответствует равенство 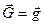 , где
, где 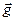 – ускорение силы тяжести.
– ускорение силы тяжести.
Перейдем теперь к рассмотрению поверхностных сил. Пусть 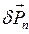 – главный вектор силы, приложенной, с одной стороны, к площадке
– главный вектор силы, приложенной, с одной стороны, к площадке 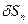 . Индекс «n» означает не проекцию силы, а указание на то, что сила действует на площадке
. Индекс «n» означает не проекцию силы, а указание на то, что сила действует на площадке 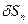 , произвольно ориентированной в пространстве. Целесообразно ввести в рассмотрение вместо силы напряжение:
, произвольно ориентированной в пространстве. Целесообразно ввести в рассмотрение вместо силы напряжение:
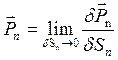 . (2.2)
. (2.2)
Рассмотрим тетраэдр, три грани которого параллельны координатным, плоскостям, а четвертая ориентирована произвольным образом (рис. 2.1).
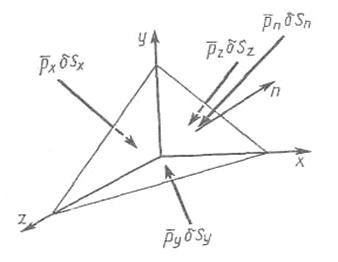 |
Рис.2.1 Тетраэдр
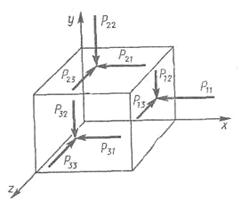 |
Рис. 2.2 Единичный куб
Обозначим площади граней 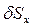 ,
, 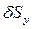 ,
, 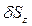 и
и 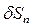 , геометрический смысл которых ясен из рисунка 2.1. Ориентация площадки
, геометрический смысл которых ясен из рисунка 2.1. Ориентация площадки 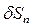 определяется единичной нормалью
определяется единичной нормалью 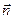 с направляющими косинусами пх, пу, пг. Тогда справедливы соотношения
с направляющими косинусами пх, пу, пг. Тогда справедливы соотношения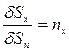 ,
, 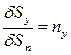 ,
, 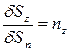 . Пусть высота тетраэдра равна h. Тогда его объем равен
. Пусть высота тетраэдра равна h. Тогда его объем равен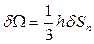 . Воспользуемся вторым законом Ньютона и составим уравнение движения тетраэдра:
. Воспользуемся вторым законом Ньютона и составим уравнение движения тетраэдра:
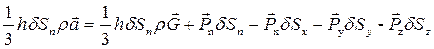 ,
,
где 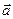 – ускорение центра масс тетраэдра.
– ускорение центра масс тетраэдра.
Переходя теперь к пределу (устремляя 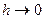 ), получим:
), получим:
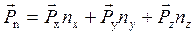 (2.3)
(2.3)
Получили формулу Коши, утверждающую, что на гранях образуется система взаимно уравновешенных напряжений. Проектируя векторное уравнение (2.3) на оси координат, получим три скалярных уравнения:
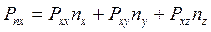 ,
,
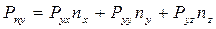 , (2.4)
, (2.4)
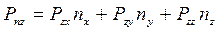 .
.
Это означает, что напряженное состояние в произвольной точке сплошной среды характеризуется девятью компонентами, образующими тензор второго ранга или диаду:
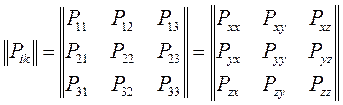 ,
,  (2.5)
(2.5)
У этого тензора имеются следующие свойства:
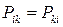 , (2.6)
, (2.6)
т.е. тензор напряжений в произвольной точке пространства обладает свойством симметрии (теорема Коши о взаимности касательных напряжений). Он содержит лишь шесть независимых компонентов.
В случае отсутствия касательных напряжений давление в точке является скалярной величиной, т.е. оно не зависит от ориентации площадки, проходящей через рассматриваемую точку.
 2014-02-02
2014-02-02 5805
5805
