Понятие элементарной жидкой частицы

МАТЕМАТИЧЕСКИЕ МОДЕЛИ ТЕЧЕНИЙ КАПЕЛЬНОЙ ЖИДКОСТИ

ЖИДКОСТЕЙ

Тема 3. МАТЕМАТИЧЕСКИЕ МОДЕЛИ ТЕЧЕНИЙ КАПЕЛЬНЫХ

Вопросы для самопроверки по темам 1,2

1. Опишите известные вам агрегатные состояния вещества.
2. Перечислите характерные точки на диаграмме состояния жидкость-пар.
3. Адибата Тейта.
4. Чем обуславливается свойство вязкости жидкости? Закон Ньютона о касательных напряжениях.
5. Объясните явление поверхностного натяжения. Коэффициент поверхностного натяжения.
6. Формула Лапласа.
7. Сущность подобия двух явлений. Виды подобий. Какие вам известны критерии подобия?

(Лекций 4 ч., СРС 4 ч.)

Два способа описания движения жидкости. Переменные Эйлера и Лагранжа.

Законы сохранения. Течение невязкой жидкости. Уравнения Эйлера.

Интеграл Бернулли.

Граничные условия на твердых стенках и на жидких поверхностях раздела. Кинематическое и динамическое условие на свободной поверхности.

Концепция потенциального течения и пограничного слоя. Кинематика потенциальных течений. Уравнение Лапласа. Краевые задачи для потенциала скорости и функции тока.

Интеграл Коши-Лагранжа.

Граничные условия на свободных поверхностях при потенциальном течении Разделение задачи на статическую и динамическую при отсутствии свободных поверхностей.

Изотермическое движение вязкой несжимаемой жидкости. Уравнения Навье-Стокса. Турбулентные течения. Подходы Рейнольдса и Колмогорова. Проблема замыкания.

ОСНОВНЫЕ ГИПОТЕЗЫ И ПОНЯТИЯ СПЛОШНОЙ СРЕДЫ. СИСТЕМА КООРДИНАТ

Классическая гидромеханика основана на трех утверждениях:

1) Справедлива классическая механика Ньютона: движе­ния происходят со скоростями, малыми по сравнению со скоростью света, и рассматриваются макроскопические объекты, размеры которых многократно превосходят размеры микромира.

2) Справедлива классическая термодинамика: предполагается, что в окрестности каждой точки жидкость находится в состоянии термодинамического равновесия или близком к нему, вследствие чего можно пользовать­ся термодинамическими законами.

3) Справедлива гипотеза сплошности: она предполагает замену реальной жидкости с ее дискретной молекулярной структурой мо­делью сплошного распределения вещества по рассматриваемому объему. Возможность такой замены и носит название гипотезы сплошности.

Выделим объем жид­кости 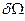,ограниченный поверхностью 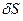, и будем считать, что в нем заключена масса жидкости 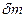. Средняя плотность жидкости может быть определена как 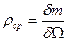. Если объем 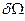достаточно велик, то в силу неоднородности среды средняя плотность будет зависеть от 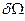. По мере уменьшения объема 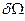распре­деление масс будет все более однородным, и средняя плотность бу­дет постепенно приближаться к некоему постоянному значению. Как только линей­ные размеры выделенного объема жидкости станут сопоставимы с размерами молекул, средняя плотность вновь начнет испытывать резкие колебания, так как в объёме 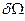может находиться разное число молекул. Отсюда возникает определение элементарной жидкой частицы (или просто частицы). Ее размеры должны быть пренебрежимо малы по сравнению с характерными размерами изучаемого тече­ния, вследствие чего средние характеристики жидкости по объему будем считать постоянными. С другой стороны, размеры частицы должны быть так велики, чтобы не учитывать молекулярную структуру жидкости. В таком случае говорят о физически бесконечно малом объеме жидкости, эффективно равном нулю. Сфор­мулированное определение частицы позволяет говорить о характе­ристиках сплошной среды в данной точке. Здесь следует сразу подчеркнуть принципиальное различие между элементарной жидкой частицей, стягиваемой в точку, и точкой пространства.

Совокупность одних и тех же жидких частиц, во все время дви­жения остающихся на одном контуре, поверхности или в объеме, называется соответственно жидким контуром, жидкой поверхностью или жидким объемом.

Итак, согласно гипотезе сплошности, жидкость моделируется непрерывной сплошной средой. С математической точки зрения это означает, что функции, характеризующие состояние среды, должны быть непрерывными и диффе­ренцируемыми в пространстве и времени. Нарушение непрерывно­сти допускается лишь на отдельных линиях или поверхностях.