Диполь

Вихрь.

Рассмотрим плоское течение от вихря:

,

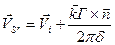где 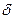- радиус цилиндра, окружающего особую точку.:

--++ + ++.

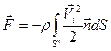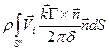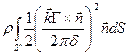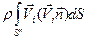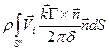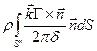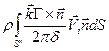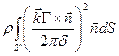Все интегралы обращаются в нуль, кроме одного.

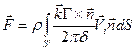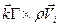=. (2.100)

Полученный результат выражает теорему Жуковского о подъемной силе. Пусть 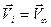. Тогда можно сформулировать следующий результат: на вихрь, помещенный в однородный поток жидкости, имеющий скорость 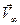, действует поперечная сила, направление которой зависит от знака циркуляции. Если циркуляция отрицательна (вращение по часовой стрелке), сила направлена вверх и называется подъемной силой:

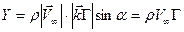, (2.101)

так как 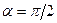и .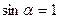

Поскольку задача плоская, сила и циркуляция относятся к единице длины, перпендикулярной плоскости чертежа.

Силы, обусловленные наличием в потоке циркуляции, относят к силам циркуляционной природы.

Как отмечалось в разделе «Кинематика», диполь можно рассматривать как совокупность источника и стока. Это позволяет простым образом выполнить качественный анализ воздействия жидкости на диполь. В самом деле, пусть ось диполя направлена под углом ε к скорости потока 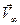. Тогда источник дает силу «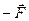», а сток — силу «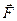». Суммарная сила будет равна нулю. Момент же не будет равен нулю 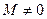. Расчетные формулы можно получить указанным путем.