Источник

Пусть в точке 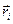расположения особенности скорость, обусловленная всеми причинами, за исключением самого источника, равна 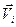. Тогда скорость на сфере радиуса 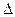, окружающая точку 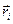, можно выразить в виде

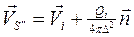. (2.98)

Найдём

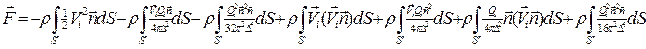
На поверхности сферы 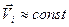, 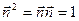. Первый, третий, четвёртый и седьмой интегралы равны нулю. Второй и пятый интегралы взаимно уничтожаются. Поэтому

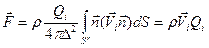. (2.99)

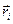Полученный результат составляет содержание частной теоремы Лагалли: источник мощности , находящийся в точке , при наличии неподвижного тела и других источников действует на тело с силой 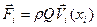, линия действия которой проходит через источник, где 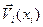- скорость, обусловленная всеми причинами, кроме самого источника. Результирующая сила от нескольких источников, действующая на тело со стороны жидкости, равна сумме сил .

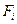Если теперь рассмотреть силу воздействия жидкости на источник, помещённый в равномерный поток 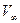, то . Сила направлена против потока (тяга).

Для стока соответственно имеем

.

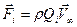Сила направлена здесь по потоку (сопротивление). Часто такое сопротивление называют сопротивлением захвата.

Обратим внимание, что анализ сил выполнен для пространственного течения. Естественно, что аналогичные выводы получаются и для плоских течений.