Формы выражения гидродинамических сил и моментов

Гидродинамические силы 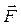и моменты ,действующие со стороны жидкости на тело, представляют собой результирующие сил давления и сил трения на поверхности движущегося тела. Обычно векторы 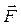и выражают через их проекции на скорост­ную или связанную системы координат.

В скоростной системе координат

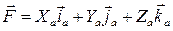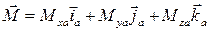; (2.144)

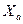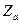Каждая из проекций носит определенное наименование: ­- лобовое сопротивление, - подъемная сила, - боковая сила, М_ха - момент крена, М_уа - момент рыскания, M_za - момент тан­гажа.

В связанной системе координат

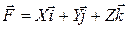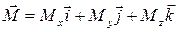; (2.145)

Проекция Х - продольная (осевая) сила, У - нормальная сила, Z - поперечная сила. Компоненты вектора момента в связанной системе координат имеют те же наименования, что и в скоростной системе координат. За положительное направление момента при­нимается такое, когда момент стремится повернуть тело против часовой стрелки (если смотреть из конца вектора).

Составляющие гидродинамической силы и момента в обеих системах координат связаны между собой и могут быть получены пересчетом. Например

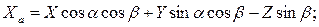
При отсутствии скольжения (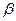=0) имеем

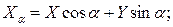
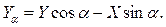
Гидродинамическую силу 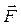и момент в соответствии с тео­рией подобия целесообразно выражать в безразмерном виде:

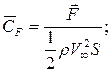
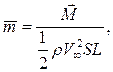(2.146)

где 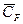и 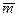- соответственно, векторные коэффициенты гидродинамической силы и момента; 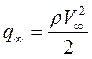- скоростной напор невозмущенного потока; S - характерная площадь тела; L - характерный линейный размер.

Обычно используют один из трех типов характерной площа­ди:

1) площадь смоченной поверхности тела S_см;

2) площадь наибольшего поперечного сечения тела (площадь миделя) S_мид и 3) площадь, вычисленную по объему тела 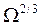. Следо­вательно,

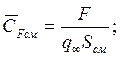
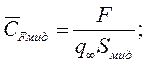
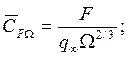
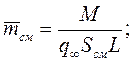
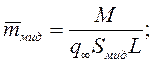
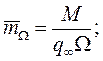
В количественном выражении для одной и той же силы или момента коэффициенты при разных условиях сравнения будут отличаться. Поэтому надо внимательно относиться к величинам безразмерных коэффициентов, учитывая условия их вычисления. Выбор той или иной характерной площади оправдывается физиче­ским смыслом или проектно-конструкторскими соображениями. В самом деле, если анализируется продольное обтекание пласти­ны, то единственная сила - сила трения. Поэтому коэффициент гидродинамической силы, вычисленный по смоченной поверхности, будет характеризовать уровень потерь в пограничном слое, т. е. степень совершенства организации пристенного течения. То же самое можно сказать и о силах трения на поверхности простран­ственного тела.

Использование объемов в качестве параметра сравнения будет характеризовать плотность компоновки, а площадь миделя отра­жает плотность использования поперечного сечения.

В дальнейшем для краткости мы будем использовать следующие термины: коэффициент гидродинамической силы или момента по смочен­ной поверхности (по миделю, по объему), имея в виду определение выше.

Безразмерные коэффициенты 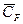и 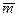должны зависеть от без­размерных гидродинамических критериев: чисел Рейнольдса, Фру­да, Вебера и др., формы тела, а также от кинематических пара­метров движения тела. Последние принимаются в качестве основ­ных параметров, от которых зависят коэффициенты 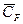и .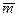

Кинематические параметры движения тела записываются в безразмерном виде в связанной системе координат:

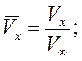
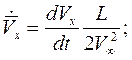
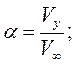
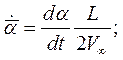
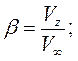
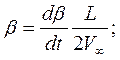
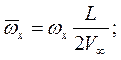
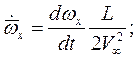
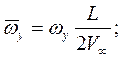
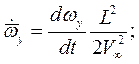
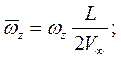
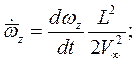
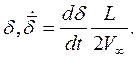
Здесь 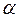, 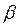- углы атаки и скольжения; 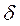- угол отклонения рулей.

Таким образом, можно записать общую функциональную зави­симость

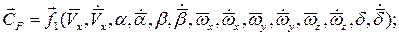
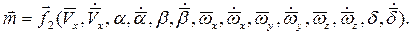
Предположим теперь, что указанные зависимости можно раз­ложить в ряд Тейлора в окрестности точки, определяемой неко­торыми значениями начальной скорости 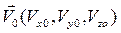и ну­левой угловой скоростью 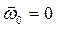. Ряд будет состоять из произведений производных гидродинамических коэффициентов по кинематическим параметрам на значения этих параметров (в пренебрежении членами высшего порядка малости). Для определенности запишем

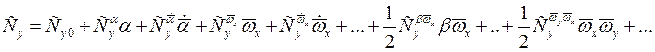
Производные, входящие в эти разложения, называются производными устойчивости.