Уравнения относительного покоя жидкости

Если в уравнениях движения жидкости в подвижной системе координат, движение которой характеризуется вектором скорости 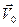начала подвиж­ной системы координат и вектором 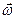угловой скорости вращения этой системы, положить равным нулю вектор относительной ско­рости движения жидких частиц, то получим уравнение относи­тельного покоя жидкости:

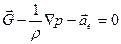(3.7)

где 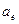— переносное ускорение, которое равно сумме ускорения полюса, вращательного ускорения рассматриваемой точки и ее осестремительного ускорения:

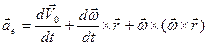, (3.8)

— вектор сил тяжести.

Как видим, основное отличие между уравнением абсолютного покоя (3.1) и уравнением относительного покоя (3.7) состоит в наличии в последнем уравнении дополнительного члена, пред­ставляющего собой переносное ускорение.