Рис. 3.5 Криволинейная стенка
Криволинейная стенка
Гидростатический парадокс
Рис.3.4
Как следует из (3.13), суммарная сила давления на площадку определяется только высотой столба жидкости. Это приводит к гидростатическому парадоксу, согласно которому силы воздействия жидкости на основания (донышки) сосудов различной формы, имеющих равные площади и одинаковые высоты столбов жидкости, одинаковы (рис. 3.4). Силы не зависят от формы сосудов.
Спроектируем криволинейную площадку S на координатные плоскости
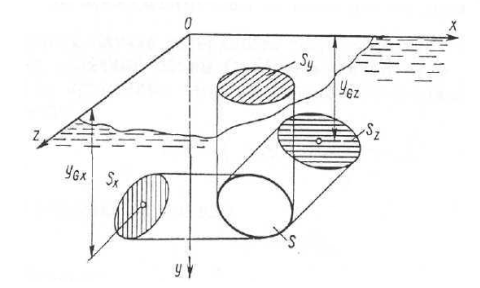
и получим проекции Sx, Sy и Sz (рис. 3.5). Давление жидкости на указанные площадки дает соответствующие компоненты главного вектора.
На основании (3.13)
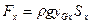 , (3.17)
, (3.17)
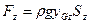 , (3.18)
, (3.18)
где 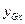 - ордината центра тяжести площадки
- ордината центра тяжести площадки 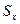 ;
; 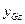 — ордината центра тяжести площадки
— ордината центра тяжести площадки 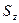 .
.
В вертикальном направлении на криволинейную площадку будет действовать вес жидкости, заключенный в объеме, ограниченном площадкой 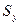 , площадкой S и вертикальной цилиндрической поверхностью, проходящей через контуры этих площадок. Образованное таким образом тело носит название тела давления. Данному определению можно придать математическую формулировку:
, площадкой S и вертикальной цилиндрической поверхностью, проходящей через контуры этих площадок. Образованное таким образом тело носит название тела давления. Данному определению можно придать математическую формулировку:
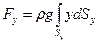 (3.19)
(3.19)
Таким образом, суммарная сила, воздействующая на криволинейную незамкнутую поверхность, может быть выражена формулой
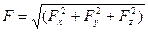 ,
,
а направление ее действия будет характеризоваться направляющими косинусами:
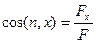 ,
, 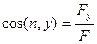 ,
, 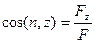
В данном случае поверхность твердой стенки замкнута и ограничивает конечный объем 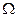 . Поэтому к поверхностному интегралу (3.9) применима теорема Гаусса—Остроградского и на основании уравнения абсолютного покоя можно получить:
. Поэтому к поверхностному интегралу (3.9) применима теорема Гаусса—Остроградского и на основании уравнения абсолютного покоя можно получить:
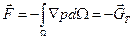 (3.20)
(3.20)
где 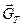 -вектор силы веса жидкости в объеме погруженного в нее тела.
-вектор силы веса жидкости в объеме погруженного в нее тела.
Полученный результат носит название закона Архимеда. Он гласит: главный вектор сил давления жидкости на поверхность погруженного в нее тела равен по модулю весу жидкости в объеме тела и направлен снизу вверх, против силы веса. Вектор 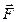 называют архимедовой силой или гидростатической подъемной силой и обозначают
называют архимедовой силой или гидростатической подъемной силой и обозначают 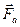 .
.
Выясним линию действия архимедовой силы.
Главный момент сил давления жидкости на погруженное тело будет равен
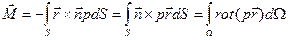
Используя свойства ротора, выражение для вектора-радиуса 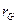 центра тяжести вытесненного объема и на основании уравнения абсолютного покоя получим:
центра тяжести вытесненного объема и на основании уравнения абсолютного покоя получим:
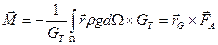 (3.21)
(3.21)
Таким образом, линия действия архимедовой силы проходит через центр тяжести вытесненного телом объема жидкости.
Если тело погружено в жидкость частично - архимедова сила будет определяться объемом погруженной части тела. Аналогично при погружении тела в несколько слоев жидкости разной плотности.
 2014-02-02
2014-02-02 880
880








