Плоская стенка

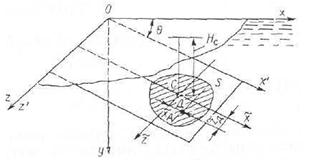
Пусть на произвольной глубине под произ­вольным углом к горизонту 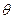расположена плоская твердая по­верхность площадью S (рис. 3.3). В данном случае на стенку действует система параллель­ных сил и, следовательно, по законам статики можно определить их равнодействующую.

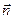Из (3.11), поскольку =const, следует:

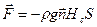
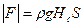(3.13)

Рис 3.3 Плоская стенка

где 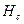- глубина центра тяжести площадки.

Таким образом, следует важный вывод: независимо от ориентации плоской стенки на нее действует сум­марная сила гидростатического давления, равная весу цилиндри­ческого столба жидкости с площадью основания, равной площади стенки S, и высотой, равной глубине центра тяжести площадки.

Определим точку приложения равнодействующей сил давления, для чего воспользуемся теоремой о моменте равнодей­ствующей силы:

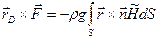(3.14)

где 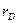- вектор-радиус центра давления (точки приложения равнодействующей).

Введем новую систему координат 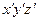, совместив плоскость 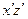с плоскостью твердой стенки (рис. 3.3). Связь между старыми и новыми координатами определяется формулами

, ,

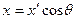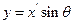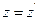
Спроектируем векторное соотношение (3.14) на оси новой системы координат:

; ;

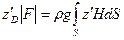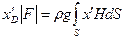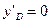
или

; ;

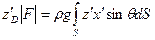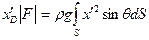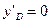
Вспоминая выражение для 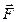, получим

; ;

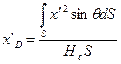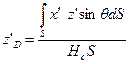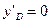
Заметим, что

.

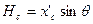Таким образом получаем:

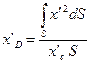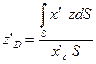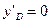; ; (3.15)

Используя выражения для 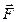, и в соответствии с теоремой о мо­ментах инерции твердого тела относительно параллельных осей .

;

,

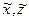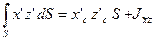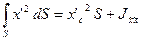где - центробежный момент и момент инерции площади в системе координат с началом в центре тяжести площадки,

получим соотношение:

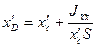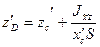; (3.16)

т.е. центр давления расположен ниже центра тяжести

площадки.