Задача об архимедовой силе как часть общей гидродинамической задачи

Как было сформулировано ранее, общая задача об изотерми­ческом движении вязкой несжимаемой жидкости записывается в виде

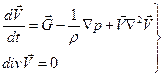(3.22)

При отсутствии свободных границ в краевые условия входят только скорости. Поэтому имеется возможность исключить из уравнений движения массовые силы 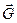. Для этого представим давление 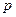в виде двух слагаемых: одно из которых будет опре­деляться гидростатикой, а другое — движением жидкости. Назовем второе слагаемое модифицированным давле­нием. Итак, положим

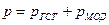
Тогда исходную систему можно разбить на две:

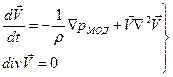(3.23)

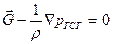(3.24)

Нетрудно видеть, что второе уравнение при решении даст архимедову силу. В то же время система (3.23), описыва­ющая течение жидкости, уже не содержит массовых сил.

В дальнейшем при рассмотрении движения тела в безгранич­ной жидкости мы не будем учитывать массовую силу (силу тяже­сти). Однако при этом будем автоматически добавлять к числу внешних сил, действующих на тело, архимедову силу.