Ламинарный пограничный слой

СОПРОТИВЛЕНИЕ ТРЕНИЯ ПРОДОЛЬНО ОБТЕКАЕМОЙ ПЛАСТИНЫ

Тема 8. ГИДРОДИНАМИЧЕСКИЕ СИЛЫ И МОМЕНТЫ, ОБУСЛОВЛЕННЫЕ ВЯЗКОСТЬЮ ВОДЫ

Вопросы для самопроверки по ТЕМЕ

1. Что понимается под несущими способностями крыла?
2. Подсасывающая сила. Причины и условия появления.
3. Вихревая система крыла конечного размаха.
4. Физика возникновения индуктивного сопротивления.
5. Особенности крыльев малого, среднего и большого удлинения.
6. Опишите процесс управления и стабилизации.
7. Поясните явление интерференции. Приведите примеры.
8. Шарнирный момент, возникающий на руле.

(Лекций 4 ч., СРС 4 ч.)

Сопротивление трения и сопротивление формы. Тела удобообтекаемые и плохообтекаемые.

Основные понятия ламинарного и турбулентного пограничного слоя. Многослойные схемы турбулентного пограничного слоя.

Зависимость сопротивления трения пластины и тела вращения. Принцип эквивалентной пластины. Влияние удлинения на сопротивление тел вращения.

Влияние вязкости на поперечные силы и моменты. Модифицированная теория тонкого тела.

При больших числах Рейнольдса на пластине формируется по­гранслой различного типа (рис. 6.1). В носовой части возникает ламинарный погранслой (участок 1), далее вниз по потоку возникает переходный погранслой (участок 2), а за ним — турбулентный погранслой (участок 3).

Расчет сопротивления целесообразно вести методами теории погранслоя. Задача упрощается тем, что отсутствует про­дольный перепад давления (dp/dx=0). Расчет течения на каждом из участков отличается рядом признаков. Рассмотрим последова­тельно методы расчета.

Течение в стационарном лами­нарном погранслое описывается одним дифференциальным уравнением в частных производных относительно функции тока 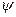(х, у) с соответствующими граничными условиями. Чис­ленные методы интегрирования позволяют найти его решение не­посредственно или после предварительного преобразования в обыкновенное дифференциальное уравнение (Блазиус). К настоящему времени составлены подробные таблицы характеристик течения в безградиентном ламинарном пограничном слое. Аппроксимация численных решений дает следующие зависимости:

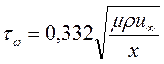
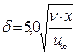
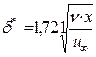
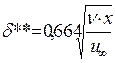
Теория пограничного слоя справедлива при больших числах Рейнольдса, a Re_x=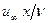при малых значениях х мало.

Выделим условно теперь пластину единичной ширины, длины L и вычислим ее суммарное сопротивление трения:

X_тр=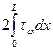=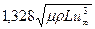(6.1)

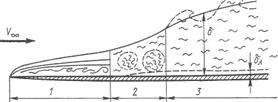
Рис. 6.1. Пластина.

а также коэффициент сопротивления трения пластины:

С_xF=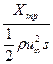= 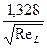(6.2)

Здесь S=2L *l, Re_L =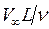. Формула (6.2) носит название формулы Блазиуса. Опытами установлена ее пригодность до Re_L=2...2,5*10⁵.