Интерференция стабилизаторов с корпусом

Простейшая модель обтекания в рамках идеальной жидкости получается в предполо­жении, что крыло (стабилизатор) с нулевой стреловидностью установлено на цилиндрическом корпусе (рис.5.26). Будем считать, что распределение циркуляции по размаху крыла Г(z) зада­но. Заменим крыло несущей линией, с которой стекают свободные вихри. Для удовлетворения условия непротекания на корпусе вос­пользуемся методом несимметричного отражения. В плоском те­чении от вихря условие непротекания на прямолинейной твердой стенке можно удовлетворить, разместив симметрично вихрь той же циркуляции, но с противоположным знаком. В случае твердой границы в виде окружности этот принцип сохраняется, но точка, в которой должен располагаться отраженный вихрь, выбирается по правилу инверсии:

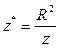(5.32)

Таким образом, вихревой системе крыла поставим в соответст­вие отраженную вихревую систему внутри корпуса. Нетрудно уви­деть, что подъемная сила крыла равна

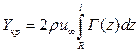(5.33)

а подъемная сила корпуса, обусловленная наличием крыла, будет

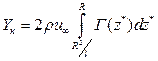(5.34)

C учетом производной функции и Г(z*)=Г(z) получим:

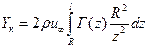(5.35)

Таким образом, суммарная подъемная сила равна

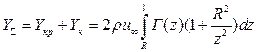
Взаимное влияние удлинения крыла и относительного радиуса корпуса отражено с помощью коэффициентов интерференции.

Если крылья-стабилизаторы имеют сужение, то эффекты ин­терференции проявляются силь­нее. В этом случае большая часть площади крыла находится в непосредственной близости от корпуса, т. е. в зоне наибольших индуцированных углов атаки. Поэтому и прирост подъемной силы будет больше. С другой стороны, и крыло будет оказывать более заметное влияние на кор­пус. Указанный эффект учитывается дополнительным множителем