Масштабный эффект. Рассмотренная модель возникновения кавитации является идеальной

Рассмотренная модель возникновения кавитации является идеальной. Она не учитывает многочисленные реальные факторы, которые могут значительно исказить картину течения. При определении начала кавитации на эталонном теле вращения в различных лабораториях мира наблюдается существенный разброс экспериментальных значений начального числа кавитации. В диапазоне скоростей потока воды 6…22 м/с начальные числа кавитации расположены в интервале σ=0,4…0,6. Все неучтённые факторы относят к масштабному эффекту.

На возникновении кавитации отражается шероховатость поверхности. Многочисленные эксперименты позволили установить эмпирическую зависимость для начального числа кавитации одиночной шероховатости:

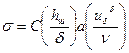. (7.4)

Здесь h_ш - высота шероховатости; δ - толщина пограничного слоя; u_δ – скорость на границе погранслоя. Константы определены для шероховатости различного вида, например, для полусфер С =0,0106 а =0,439 b =0,298 для конусов C =0,0338 a =0,632 b =0,451.

Если одиночная шероховатость расположена на криволинейной поверхности тела вращения, то соответствующее начальное число кавитации определяется как

σ=-C_р.ш+(1-С_р.ш)/σ_ш, (7.5)

где С_р.ш – коэффициент давления в месте расположения шероховатости, рассчитанный по потенциальной теории для гладкой поверхности.

При наличии распределенной шероховатости начальное число кавитации тесно связано с местным коэффициентом трения С_xf:

σ₂=16C_xf. (7.6)

Течение в донной области за плохообтекаемыми телами характеризуется интенсивными вихревыми образованиями. В ядрах вихрей может возникнуть пузырьковая кавитация. Начальные числа кавитации в этом случае выражают формулами вида

σ_вихр=a+b(Re)ⁿ,

коэффициенты которых находят полуэмпирическим путем. В частности, для диска с острыми кромками найдено

σ_вихр=0,44+0,00036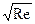. (7.7)