Открытые (незамкнутые) схемы

Классические схемы развитых кавитационных течений

1) Схема Кирхгофа

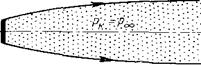
В течениях данного типа либо сама каверна, либо след от нее простираются в бесконечность. Чрез­вычайно важную роль играет каверна Кирхгофа, границы которой уходят в бесконечность (рис. 7.5). Таким образом, ско­рость на границах должна быть равной скорости на бесконечности (V_k=V_∞) и соответственно давление в каверне должно быть равно давлению на бесконечности (рк=р_∞). Но это означает, что беско­нечная каверна Кирхгофа соответствует нулевому числу кавитации (σ=0).

Рис. 7.5 Каверна Кирхгофа

Б. Бетц распространил данную схему на числа кавитации, отличные от нуля, предположив, что с наветренной сто­роны тела-кавитатора и в этом случае сохранится такое же распре­деление давления, как и в схеме Кирхгофа, а в каверне давление будет отличаться от давления на бесконечности (р_к≠р_∞). Данный подход сразу же позволяет получить формулу для сопротивления при ненулевых числах кавитации, носящую имя Бетца:

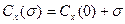(7.9)

Однако данная схема не строга, а в дальнейшем выяснилось, что формула (7.9) пригодна лишь для очень острых конусов.

2) Схема Жуковского-Рошко (рис. 7.6)

Рис. 7.6 Схема Жуковского-Рошко.

Эта схема базируется на решении Жуковского о поперечном отрывном обтекании пластины в присутствии двух бесконечных параллельных стенок (плоской трубы). Согласно этой схеме, стенки каверны, на которых выполняется условие p_k=const, причём 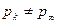, замыкаются на параллельные набегающему потоку твёрдые пластины. На твёрдых стенках давление восстанавливается от значения p_k до p_{∞ .}

Развитием этой схемы является схема Ву-Фабулы, в которой каверна замыкается на жидкий след постоянной ширины, положение которого в пространстве определяется специальными граничными условиями.