Стационарные и нестационарные каверны.
ОСНОВНЫЕ ДОПУЩЕНИЯ И СХЕМЫ ТЕЧЕНИЯ КЛАССИЧЕСКОЙ ТЕОРИИ РАЗВИТОЙ КАВИТАЦИИ
Классическая теория развитой кавитации содержит в своей основе следующие допущения:
1) жидкость считается идеальной, несжимаемой, невесомой;
2) давление в каверне принимается постоянным;
3) течение рассматривается стационарным.
Для построения границ развитых каверн Бриллюэн сформулировал два принципа, которые во многом определили дальнейшее развитее теории:
1) на стенках каверны существует постоянное и минимальное давление;
2) границы каверны должны описываться простыми несамопересекающимися кривыми (поверхностями), не пересекающими контуры обтекаемого тела.
В реальных условиях течение жидкости в кормовой части каверны всегда является нестационарным и не поддается теоретическому описанию. В то же время при стационарном набегающем потоке стенки кавитационной полости на большой протяженности головной части имеют четко выраженный стационарный характер. Поэтому для получения практически полезных решений в таких случаях вводят понятие стационарной каверны. Иными словами, стационарная каверна соответствует стационарным условиям в набегающем потоке и стационарному положению тела - кавитатора. Нестационарные процессы в кормовой части не учитываются.
Однако нестационарность может возникнуть и по другим причинам: либо вследствие неравномерного движения тела - кавитатора (ускорения, замедления, колебаний относительно равновесного положения), либо от изменения давления в каверне со временем и т. д. В этих случаях говорят о нестационарных кавернах. Важно отметить, что и в этом случае нестационарные процессы разрушения стенок каверны в кормовой части не рассматриваются.
Из первого принципа Бриллюэна следует, что скорость на границе каверны постоянна и равна
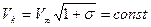 (7.8)
(7.8)
В то же время при выпуклой стационарной каверне конечных размеров в кормовой области должна существовать задняя критическая точка, скорость в которой равна нулю. Таким образом, налицо противоречие: граничное условие (7. 8) в одной точке не выполняется. Это противоречие получило название парадокса Бриллюэна. Следствием из него является утверждение: стационарную каверну конечных размеров построить невозможно. Таким образом, основной проблемой построения схемы стационарной каверны оказалось замыкание границ каверны в хвостовой части.
 2014-02-02
2014-02-02 637
637








