Плоские задачи развитых кавитационных течений

Схема каверн с отрицательными числами кавитации.

Сопоставление различных кавитационных схем.

Полуоткрытые (полузамкнутые) схемы.

В схемах этого типа каверна заканчивается одинарными или двойными спиральными вихрями (рис. 7.10), в точках расположения которых происходит изменение скорости от значения V_k до V_∞.

Сопоставление разных схем развитой кавитацией позволяет сделать следующие общие выводы:

1) Вид течения в кормовой части каверны очень мало влияет на характеристики течения в головной её части.

2) Для всех схем приблизительно одинаковыми оказываются и силовые характеристики C_x(σ), и конфигурации каверн.

Исключение по совпадению конфигурации каверн составляет схема Жуковского – Рошко. Поэтому для расчёта профиля каверн эта схема не рекомендуется.

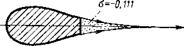
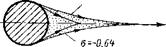
Рис.7.11(а) Рис.7.11 (б)

Не вдаваясь в причины образования полостей с повышенным по отношению к окружающей среде давлением, отметим, что они должны располагаться в зо­нах пониженных скоростей на поверхности тела, т. е. в районе критических точек. Расчетные контуры таких течений показаны на рис. 7.11. Вариант (а)соответствует профилю со срезанной кормовой частью (Лайтхилл), а вариант (б) — круговому ци­линдру (Саусвелл и Вейси). Как видим, точки отрыва ка­верны расположены на сужающихся частях тела. Каверна заканчивается точкой заострения и имеет конечную длину. Для систе­мы «тело — каверна» в идеальной жидкости, очевидно, в данном случае справедлив парадокс Даламбера, т. е. сопротивление равно нулю.

До сих пор речь шла о так называемой правильной кавитации, когда σ>0. Однако теоретически допустимы течения с σ<0 (рис.7.11). Они характерны для каверн, стенки которых примыкают к сужающимся участкам кавитирующего тела и заканчиваются заострением. Кривизна стенок каверны, очевидно, будет противоположной случаю σ>0. Нетрудно видеть, что сила сопротивления составного тела (тело+каверна) в идеальной жидкости будет равна нулю.