Алгоритм численных решений

Можно отметить два основных подхода: метод интегральных уравнений и метод конечных разностей. В качестве схем кавитационных течений обычно принимается схема Рябушинского или схема Жуковского - Рошко.

Метод конечных разностей (метод сеток) является наиболее универсальным методом решения задач гидромеханики. В методе конечных разностей вся область течения покрывается сеткой, в узлах которой записываются значения искомой функции: потенциала скорости Ф или функции тока ψ. Таким образом, осуществляется переход от непрерывной функции непрерывных аргументов к дискретной функции дискретных аргументов. Выражая в каждом узле значения функции, ее первой и второй производной через значения функции в окрестных узлах, мы получаем конечно – разностный аналог исходного дифференциального уравнения для Ф или ψ, который, как правило, сводится к системе алгебраических уравнений.

В случае прямолинейных границ расчетной области вводится равномерная прямоугольная сетка, и тогда все узлы сетки являются с точки зрения методики вычисления одинаковыми. В случае криволинейных границ расчетной области использование прямоугольной сетки затруднено, так как узлы сетки не повпадают на криволинейную границу и требуется создание специального алгоритма. С одной стороны, это снижает точность аппроксимации исходного уравнения, а с другой – увеличивает время вычислений. Поэтому при расчете обтекания криволинейных препятствий стараются вводить так называемые адаптивные сетки, в которых узлы располагаются точно на границе.

В случае кавитационного течения граница каверны является заведомо криволинейной.

Для получения численного решения кавитационных задач наиболее распространен метод интегральных уравнений.

Решение кавитационных задач происходит итерационно. В общем виде итерационный процесс можно сформировать следующим образом. На начальном шаге задается пробная форма каверны и решается прямая задача. Естественно, что условие постоянства давления на участке каверны выполняться не будет. Поэтому на следующем шаге по какому – либо аргументированному правилу производится коррекция формы каверны, и цикл расчетов повторяется. Расчеты заканчиваются, когда в пределах заданной точности форма границы перестает изменяться.

В современной вычислительной гидромеханике существует проблема наглядного и доступного представления полученных численных результатов, особенно в многомерных задачах. Типичным приемом является аппроксимация результатов параметрических расчетов сравнительно простыми зависимостями. Применительно к кавитационным течениям интерес представляют аппроскимации численных решений, полученные Гузевским для габаритов каверн около конусов и коэффициентов сопротивления конусов:

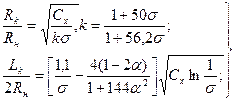(7.63)

C_x(σ)=C_x(0)+(0,524+0,672α)σ, 0≤σ≤0,25; ;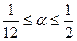

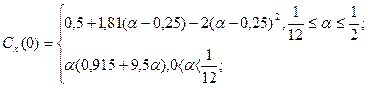
(7.64)

где απ - угол полураствора конуса.

Для диска из последних формул следует

С_х(σ)=0,8275+0,86σ.

При σ=0 получается асимптотический результат Гарабедяна.