Обтекание пластины при ненулевых числах кавитации

Коэффициент сопротивления при поперечном обтекании пластины, рассчитанной по схеме с возвратной струйкой и по схеме Рябушинского, выражается одинаковым рядом:

C_x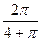(σ)=[1+σ+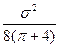+ O(σ³)]. (7.35)

В случае схемы Жуковского - Рошко в третьем члене в скобках 8 заменяется на 6. Как видим, при малых числах кавитации можно принять

C_x(σ)=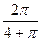(1+σ)=C_x(0)(1+σ), (7.36)

где C_x(0)=2π/(4+π)=0,88.

При σ=1 погрешность этой приближенной формулы составляет 0,8%, а при уменьшении σ ее точность возрастает.

Аналитическое поведение границ плоских каверн при σ→0 на больших расстояниях от кавитирующего тела подчиняется закону:

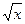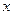y-y₀~C₁+C₂ln+O(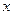^-1/2ln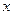). (7.37)

Габариты каверны, вычисленные по схеме Рябушинского, оцениваются формулами:

а) ширина каверны

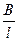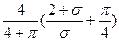~; (7.38)

б) длина каверны

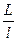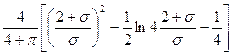~; (7.39)

в) удлинение каверны

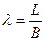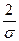~. (7.40)

Погрешность вычисления ширины каверны не превышает 0,6% при σ<3. Формула (7.39) дает завышенные результаты длины каверны на 0,7% при σ=1.

Линейная зависимость коэффициента сопротивления от числа кавитации характерна также и для коэффициента подъемной силы. Эта же закономерность оказывается действительной и в пространственных течениях.

Наряду со сказанным необходимо подчеркнуть, что зависимость C_x(σ)=C_x(0)(1+σ) хорошо отражает силовое взаимодействие с потоком сильно затупленных тел, образом которых была пластина, установленная поперек потока. Для заостренных тел линейная зависимость сил от числа кавитации сохраняется, но ее точнее записать в форме

C_x(σ)=C_x(0)(1+βσ), (7.41)

где β- поправочный множитель, зависящий от формы тела. При этом C_x(0), естественно, также зависит от конфигурации тела. Частным примером может служить известная формула Бетца для острых клиньев (конусов):

C_x(σ)=C_x(0)+σ. (7.42)