Математическая модель течения

ОСЕСИММЕТРИЧНЫЕ ТЕЧЕНИЯ С РАЗВИТОЙ КАВИТАЦИЕЙ. ЧИСЛЕННЫЕ И ПРИБЛИЖЁННЫЕ МЕТОДЫ РАСЧЁТА

Осесимметричные кавитационные течения относятся к разряду наиболее изученных с теоретической и экспериментальной точек зрения. Этому способствовала двухмерность течения. В то же время осесимметричные течения, по существу, являются пространственными и вследствие этого обладают специфическими чертами. Для определения конфигурации осесимметричных каверн и силовых характеристик кавитационных течений расчетным путем необходимо, как и в плоских течениях, разрешить проблему замыкания каверны. Для расчёта используются аналитические методы решения и численные методы, а так же полуэмпирические методы расчёта.

Рассмотрим осесимметричное обтекание однородным потоком со скоростью V_∞ составной конфигурации: «тело – каверна – замыкатель». Введем неподвижную, связанную с телом цилиндрическую систему координат (x,r,θ), начало которой совместим с носиком тела - кавитатора. Пусть r=T(x) и r=R(x) - уравнения меридионального сечения тела и каверны на схеме соответственно. В целях упрощения изложения остановимся лишь на схеме Рябушинского «с зеркалом», а отрыв будем считать фиксированным.

Во всей области течения справедливо уравнение Лапласа для потенциала скорости:

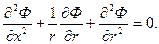(7.43)

Компоненты скорости жидкой частицы выражаются через потенциал скорости следующим образом:

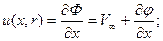(7.44)

υ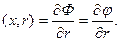 (7.45)

Запишем теперь граничные условия на поверхности составного тела, часть геометрии которого известна (тела, замыкателя), а другая подлежит определению (профиль каверны).

На границах твердого тела справедливо условие непротекания:

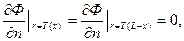(7.46)

что эквивалентно выражению

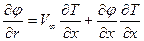при r=T(x), r=T(L-x). (7.47)

На поверхности каверны, являющейся свободной поверхностью, длжны выполняться кинематическое и динамическое условия.

Кинематическое условие:

при r=R(x). (7.48)

Динамическое условие:

p_k= const при r=R(x). (7.49)

Но из уравнения Бернулли следует

(7.50)

или в безразмерной форме

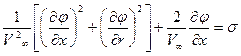, (7.51)

где σ- число кавитации.

Таким образом, динамическим условием на поверхности каверны служит соотношение (7.51)

Кинематическое условие (6.45) представляет собой условие непротекания поверхности каверны. Это обстоятельство можно использовать для получения новой формы граничного условия на поверхности каверны. Есл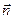и и 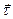– нормальное и тангенциальное направления на поверхности каверны, то уравнение Бернулли приобретает вид

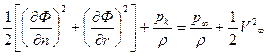
Но согласно (7.46) 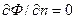. Следовательно,

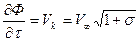, (7.52)

т.е. скорость на границе каверны V_k является постоянной, так как V_∞=const и σ=const.

Вместо потенциала скорости можно использовать функцию тока осесимметричного течения ψ, связанную с компонентами скорости соотношениями

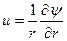; υ=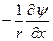. (7.53)

Для ψ справедливо уравнение

, (7.54)

Уравнение неразрывности при этом удовлетворяется автоматически. В самом деле должно быть

.

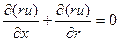Но согласно предыдущему получаем

.

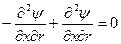В качестве граничного условия можно использовать основное свойство функции тока, согласно которому она сохраняет постоянное значение вдоль линии тока. Поэтому запишем

ψ=0 при r=0, x<0; r=T(x), r=R(x), r=T(L-x), 0<x<L; r=0, x>L. (7.55)