Аналитическая оценка решения задач

Согласно принятой классификации краевых задач, рассматриваемая задача относится к типу смешанных. На части границы конфигурация известна и требуется определить параметры течения (прямая задача гидромеханики). На остальной части границы заданы параметры течения, по которым нужно восстановить конфигурацию границы (обратная задача гидромеханики). Кавитационная задача, в которой задается условие p_k=const, является частным случаем более общей обратной задачи.

Исследовано поведение границ бесконечной осесимметричной каверны - осесиметричного аналога каверны Кирхгофа - на большом удалении от кавитирующего тела. Из условия, что сопротивление кавитирующего тела оставалось бы конечным, т.е. не обращалось бы ни в нуль, ни в бесконечность, получен следующий асимптотический закон расширения каверны:

R(x)≈Cx^1/2ln^-1/4x ,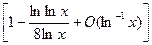

или приближенно

R(x)≈Cx^1/2ln^-1/4x. (7.56)

Сопоставляя это выражение с аналогичной формулой для плоской задачи (7.31), находим, что осесимметричная каверна является более тонкой по сравнению с плоской пропорционально множителю ln^-1/4x.

Константа С выражается через силу сопротивления тела и параметры набегающего потока

C=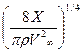. (7.57)

В уравнение для функции тока введем параметр ε:

,

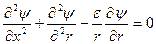так что при ε=0 получается плоская задача, а при ε=1 – осесимметричная, и построим решение в виде ряда ε

ψ(x,r,ε)=ψ₀(x,r)+εψ₁(x,r)+ε²ψ₂(x,r)+…. (7.58)

Сопротивление диска, обтекаемого по схеме Кирхгофа, оказалось равным С_x(0)=0.827.

При обтекании диска по схеме Рябушинского в случае малых чисел кавитации получены следующие асимптотические формулы:

С_x(σ)=C_x(0)(1+σ); (7.59)

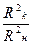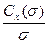~; (7.60)

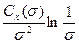~; (7.61)

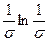~, (7.62)

где R_н – радиус диска; L_k – длина каверны; R_k – радиус миделевого сечения каверны.