Помехоустойчивое кодирование – процесс введения избыточной информации в передаваемое информационное сообщение. В сформированной кодовой последовательности должны быть информационные символы и некоторые дополнительные (проверочные) символы, т.е. помехоустойчивое кодирование является избыточным.
Помехоустойчивый код – конечное множество кодовых последовательностей, построенных по одному и тому же алгоритму.
Помехоустойчивый код характеризуют следующими параметрами:
1. Основание кода q – число элементарных символов, выбранных для передачи сообщений. Например, для двоичного и троичного кода q2={0;1}, q3={-1;0;1}.
2. Длина кода n – число символов, выбранных для передачи сообщений.
3. Число информационных позиций в коде, выбранных для передачи данных – k.
4. Число проверочных (контрольных) позиций в коде – l=n-k.
5. Кобщ=2n – общее количество кодовых последовательностей,
Краз=2к – количество разрешенных кодовых последовательностей,
Кзапр=21 – количество запрещенных кодовых последовательностей.
6. Скорость передачи кода R=k/n характеризует качество кода.
7. Относительная избыточность кода r=(n-k)/n*100%=(1-R)*100%
Абсолютная избыточность кода l=n-k
8. Вес кодовой последовательности w – количество ненулевых значений позиций кодовой комбинации F(x). Например, F(x)=011101101 Þ w=6 двоичных символов.
9. Кодовое расстояние кода d характеризует возможности кода по контролю ошибок, равно количеству несовпадений в кодовых последовательностях.
F1(x)=0111011101
Å F2(x)=1011010010
d =11 1111=6
Хэмминг доказал, что не максимальное, а минимальное кодовое расстояние характеризует корректирующие свойства помехоустойчивого кода. Минимальное кодовое расстояние обозначается как d0 или dx (хэмминговое расстояние) и равно наименьшему значению d из всей их совокупности. Cпозиции теории кодирования dx показывает, сколько символов в кодовой последовательности надо исказить, чтобы перевести ее в другую кодовую последовательность.
Определены как нижние, так и верхние границы значений dx:
- нижние границыустанавливают факт существования помехоустойчивых кодов с таким значением dx;
- верхние границы определяют максимальное теоретическое значение dx.
Нижняя граница Хэмминга определяется по формуле:
l ≥ log2(1+n+Cn2+…+Cntиспр) Þ 2 l ≥ 1+n+Cn2+…+Cntиспр
10. Кратность контролируемой ошибки t (tобн или tиспр).
d0=2 tиспр+ 1 Þ tиспр =(d0-1)/2 – количество ошибочных символов, которое может исправить помехоустойчивый код,
d0= tобн+ 1 Þ tобн =d0-1 – количество ошибочных символов, которое может обнаружить помехоустойчивый код.
Для того, чтобы помехоустойчивый код исправлял t испр ошибок и обнаруживал t o6н ошибок необходимо, чтобы d0≥ tиспр + tобн + 1
11. Вероятность ошибки декодирования
n
Рош.дек.=åСni×Pki×(1-Pk)n-I,
i=tиспр.
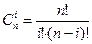 – число сочетаний, Pk – вероятность ошибки в канале связи.
– число сочетаний, Pk – вероятность ошибки в канале связи.
На практике коды, как правило, обозначают (n;k) или (n;k;d). Например, обозначение (7;4) или (7;4;3) характеризует блоковый код Хэмминга длиной n=7, числом информационных позиций k=4, кодовым расстоянием d=3.
 2014-02-02
2014-02-02 6097
6097
