Условия и свойства формирования разрешенных кодовых последовательностей ЛБК

Линейные блоковые коды

Линейным блоковым кодом называется такой помехоустойчивый код, у которого проверочные символы формируются путем суммирования по модулю два информационных символов, расположенных на определенных позициях, а сумма двух кодовых последовательностей и произведение кодовой последовательности на элемент поля образуют также кодовые последовательности.

Основные свойства ЛБК:

1. линейность кода определяется специально выбираемой структурой кода. Линейность кода существенно упрощает процедуру кодирования и декодирования, позволяя выразить каждую кодовую последовательность в виде "линейной" комбинации небольшого числа выделенных кодовых последовательностей, так наливаемых базисных векторов;

2. сумма по модулю два двух кодовых последовательностей также является кодовой последовательностью;

3. линейный блоковый код всегда содержит кодовую последовательность, состоящую целиком из нулей;

4. если сложить по модулю два некоторую кодовую последовательность со всеми кодовыми последовательностями, то снова получится множество всех кодовых последовательностей, расположенных в другом порядке;

5. вес кодовой последовательности (W_кп) всегда должен быть > d₀;

6. вес проверочной части кодовой последовательности (W_пр.ч.кп) должен быть всегда ≥ (do-l);

7. вес суммы по модулю два двух разрешенных кодовых последовательностей (W_åкп) должен быть всегда ≥ (d₀-l), но допускается ≥ (d₀-2);

8. групповой двоичный линейный блоковый код полностью задается как порождающей G_k,n (х), так и проверочной H_l,n (x) матрицами.

В ЛБК сумма по модулю два любого конечного числа разрешенных кодовых последовательностей также является разрешенной кодовой последовательностью. Поэтому, выбрав k исходных разрешенных кодовых последовательностей, которые называют базисными и суммируя их посимвольно в i различных сочетаниях, можно построить все 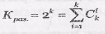разрешенных кодовых последовательностей.

Чтобы каждое сочетание порождало новую разрешенную последовательность и чтобы в конечном итоге их общее число равнялось 2^к необходимо, чтобы выполнялись следующие условия (правила):

1) исходные (базисные) кодовые последовательности должны выбираться различными;

2) нулевая кодовая последовательность (состоящая из одних 0) не должна выбираться;

3) исходные кодовые последовательности должны быть линейно-независимыми и образовывать алгебраическую группу по отношению к операции суммирования по модулю два и в том смысле они являются групповыми кодами;

4) вес (число 1) каждой исходной кодовой последовательности должен быть не менее d₀ и в общем случае вес кодовой последовательности равен числу ненулевых символов;

5) вес приписываемой проверочной части строки к исходной информационной части строки должен быть не менее d₀-1;

6) кодовое расстояние между любыми парами исходных кодовых последовательностей должен быть не менее d₀;

7) минимальное кодовое расстояние d₀ ЛБК равно наименьшему кодовому расстоянию из всей совокупности полученных кодовых расстояний (d) при попарном суммировании по модулю два двоичных символов сравниваемых последовательностей. Минимальное кодовое расстояние d₀ также будет определять и минимальный вес кодовых последовательностей конкретного, т. е. проектируемого или выбираемого кода (W_min=d₀).