Способ мажоритарного декодирования привлекает как простотой описания, так и невысокой сложностью схемной реализации. Идея мажоритарного декодирования линейного кода базируется на системе проверочных равенств, а именно, в кодах с мажоритарным декодированием каждый символ может быть выражен через другие символы несколькими способами. Это позволяет для определения истинного значения символа воспользоваться принципом большинства (мажоритарным принципом).
Существует три способа построения систем проверочных уравнений при мажоритарном декодировании:
– системы с разделенными проверками;
– системы с l- связанными проверками;
– системы с квазиразделенными проверками.
В системах с разделенными проверками некоторый символ, относительно которого разделяется система уравнений, входит во все уравнения. Любой другой символ входит не более чем в одну проверку. Отсюда следует, что для коррекции t ошибок система должна состоять из (2 t + 1) уравнений и иметь на столько же входов мажоритарные элементы.
Пример: Пусть имеется код (6; 3), задаваемый следующей проверочной матрицей:
а1а2а3 а4а5а6
0 1 1 1 0 0
H(x) =1 0 1 0 1 0
1 1 1 0 0 1
Запишем систему уравнений:
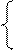 а4= a2Åa3
а4= a2Åa3
а5= a1Åa3
а6= a1Åa2Åa3
Из этой системы можно записать систему проверочных равенств, где равенство аi=аi называется уравнением истинности или тривиальным.
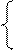 Для a1: a1= a3Åa5
Для a1: a1= a3Åa5
а1 = а2Åa3Åa6=а4Åa6
а1= a1
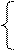 Для a2: a2= a3Åa4
Для a2: a2= a3Åa4
а2 = а1Åa3Åa6=а5Åa6
а2= a2
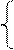 Для a3: a3= a2Åa4
Для a3: a3= a2Åa4
а3 = а1Åa5
а3= a3
Видно, что каждый из принятых символов ai входит в данные системы один раз, и, следовательно, если он ошибочен, то ошибочным будет одно из трех уравнений системы; два остальных – правильны. По большинству правильных проверок мажоритарный элемент принимает правильное решение об оценке состояния разряда.
С ростом числа корректируемых ошибок растет число уравнений в системе и, следовательно, увеличивается сложность мажоритарного элемента.
Декодер для кода (6,3) требует шесть сумматоров по модулю два и три мажоритарных элемента.
Схема мажоритарного декодера кода (6, 3) представлена на рисунке.

Рисунок – Схема мажоритарного декодера кода (6, 3)
Достоинства мажоритарного декодирования: простота реализации, высокая скорость декодирования.
Недостатки: такие декодеры могут декодировать малый класс кодов.
 2014-02-02
2014-02-02 3298
3298








