Режим работы любой цепи полностью характеризуется уравнениями, составленными на основании законов Кирхгофа. При этом необходимо составить и решить систему с n неизвестными, что может оказаться весьма трудоемкой задачей при большом числе n ветвей схемы. Однако, число уравнений, подлежащих решению, может быть сокращено, если воспользоваться специальными методами расчета, к которым относятся методы контурных токов и узловых потенциалов.
Идея метода контурных токов: уравнения составляются только по второму закону Кирхгофа, но не для действительных, а для воображаемых токов, циркулирующих по замкнутым контурам, т.е. в случае выбора главных контуров равных токам ветвей связи. Число уравнений равно числу независимых контуров, т.е. числу ветвей связи графа  . Первый закон Кирхгофа выполняется автоматически. Контуры можно выбирать произвольно, лишь бы их число было равно
. Первый закон Кирхгофа выполняется автоматически. Контуры можно выбирать произвольно, лишь бы их число было равно 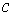 и чтобы каждый новый контур содержал хотя бы одну ветвь, не входящую в предыдущие. Такие контуры называются независимыми. Их выбор облегчает использование топологических понятий дерева и ветвей связи.
и чтобы каждый новый контур содержал хотя бы одну ветвь, не входящую в предыдущие. Такие контуры называются независимыми. Их выбор облегчает использование топологических понятий дерева и ветвей связи.
Направления истинных и контурных токов выбираются произвольно. Выбор положительных направлений перед началом расчета может не определять действительные направления токов в цепи. Если в результате расчета какой-либо из токов, как и при использовании уравнений по законам Кирхгофа, получится со знаком “-”, это означает, что его истинное направление противоположно.
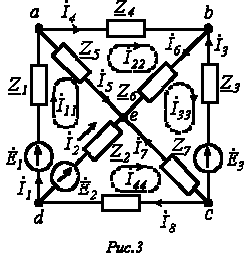
Пусть имеем схему по рис. 3.
Выразим токи ветвей через контурные токи:
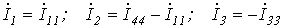 ;
;
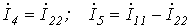 ;
;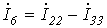 ;
;
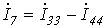 ;
; 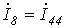 .
.
Обойдя контур aeda, по второму закону Кирхгофа имеем
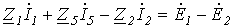 .
.
Поскольку 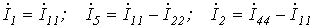 ,
,
то
 .
.
Таким образом, получили уравнение для первого контура относительно контурных токов. Аналогично можно составить уравнения для второго, третьего и четвертого контуров:
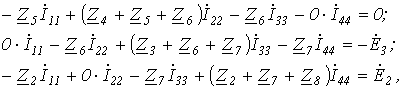
совместно с первым решить их относительно контурных токов и затем по уравнениям, связывающим контурные токи и токи ветвей, найти последние.
Однако данная система уравнений может быть составлена формальным путем:
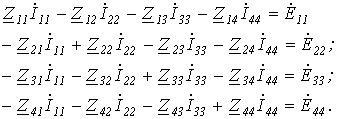
При составлении уравнений необходимо помнить следующее:
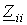 - сумма сопротивлений, входящих в i- й контур;
- сумма сопротивлений, входящих в i- й контур;
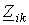 - сумма сопротивлений, общих для i- го и k- гоконтуров, причем
- сумма сопротивлений, общих для i- го и k- гоконтуров, причем  ;
;
члены на главной диагонали всегда пишутся со знаком “+”;
знак “+” перед остальными членами ставится в случае, если через общее сопротивление 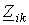 i- й и k- й контурные токи проходят в одном направлении, в противном случае ставится знак “-”;
i- й и k- й контурные токи проходят в одном направлении, в противном случае ставится знак “-”;
если i- й и k- й контуры не имеют общих сопротивлений, то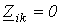 ;
;
в правой части уравнений записывается алгебраическая сумма ЭДС, входящих в контур: со знаком “+”, если направление ЭДС совпадает с выбранным направлением контурного тока, и “-”, если не совпадает.
В нашем случае, для первого уравнения системы, имеем:

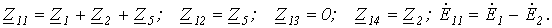
Следует обратить внимание на то, что, поскольку  , коэффициенты контурных уравнений всегда симметричны относительно главной диагонали.
, коэффициенты контурных уравнений всегда симметричны относительно главной диагонали.
Если в цепи содержатся помимо источников ЭДС источники тока, то они учитываются в левых частях уравнений как известные контурные токи: k- й контурный ток, проходящий через ветвь с k- м источником тока равен этому току 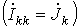 .
.
 2014-02-02
2014-02-02 1194
1194