2014-02-02
4100
Перейдем к геометрической интерпретации задачи линейного программирования с n переменными.
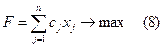
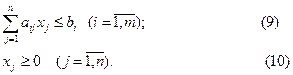
Множество планов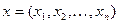 
, компоненты которых удовлетворяют ограничению-неравенству 
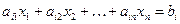, геометрически представляют собой гиперплоскость n -мерного пространства. Это выпуклое множество. Множество планов 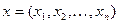, компоненты которых удовлетворяют неравенству 
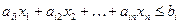, образует полупространство n -мерного пространства, которое также является выпуклым множеством. Множество планов, удовлетворяющих системе ограничений ЗЛП, представляет собой пересечение конечного числа полупространств и потому является выпуклым.
Геометрически задача сводится к нахождению точки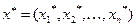 
многогранника (многоугольной области), определяемого неравенствами (9), (10), через которую проходит гиперплоскость семейства (8), соответствующая наибольшему значению F.
Графическим методом можно решить ЗЛП с n>2 переменными, если в её канонической записи число неизвестных n и число линейно независимых уравнений m связаны соотношением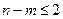 
.
В этом случае каноническую форму задачи преобразовывают в симметричную, которая будет содержать не более двух переменных. Решая эту задачу графически, находят два компонента оптимального плана. Подставляя их в ограничения задачи, определяют и остальные компоненты.
Пример. Найти
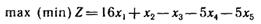
при ограничениях:
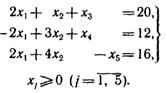
Решение. В данной задаче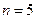 
, 
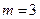. Так как 
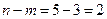, задачу можно решить графически. Решим систему ограничительных уравнений относительно любых трех неизвестных. В данном случае проще всего решить систему относительно 
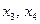и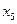 
:
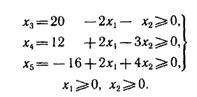
Подставив выражения для 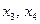и 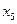в целевую функцию, после упрощений получим 
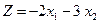. ЗЛП с двумя переменными принимает вид
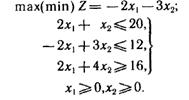
На рис. 2 представлены многоугольник решений ABCD, линия уровня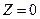 
и вектор
с = (- 2; -3).
Максимального значения целевая функция достигает в точке А (0; 4), т. е.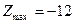 
, а минимального — в точке B (6; 8): 
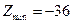. Подставив координаты точек А и В в выражения для 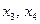, ,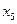найдем остальные координаты экстремальных точек: А '(0; 4; 16; 0; 0), В '(6; 8; 0; 28). При этом , .
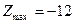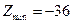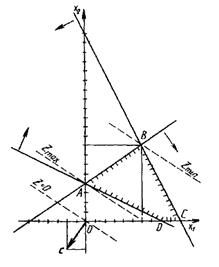
Рис. 2
