Геометрическая интерпретация, которой мы пользовались при решении задач линейного программирования, перестает быть пригодной при числе свободных переменных 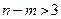 , а затруднительна уже при
, а затруднительна уже при 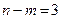 .
.
Если свободных переменных оказывается уже не две, а три 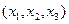 , а остальные
, а остальные 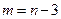 базисных переменных могут быть выражены через свободные, то геометрическую интерпретацию этой задачи придется строить уже не на плоскости, а в пространстве. Каждое условие
базисных переменных могут быть выражены через свободные, то геометрическую интерпретацию этой задачи придется строить уже не на плоскости, а в пространстве. Каждое условие 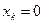 для одной из базисных переменных геометрически изобразится уже не прямой, а плоскостью. По одну сторону от этой плоскости
для одной из базисных переменных геометрически изобразится уже не прямой, а плоскостью. По одну сторону от этой плоскости 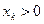 , по другую
, по другую 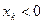 .
.
Область допустимых решений (если она существует) представляет собой выпуклый многогранник, ограниченный плоскостями.
Если 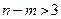 , то мы выходим за рамки трехмерного пространства, и геометрическая интерпретация теряет наглядность.
, то мы выходим за рамки трехмерного пространства, и геометрическая интерпретация теряет наглядность.
Для нахождения решения задачи линейного программирования в общем случае (при произвольном числе свободных переменных) применяются не геометрические, а вычислительные методы. Из них наиболее универсальным является симплекс-метод.
Впервые симплексный метод был предложен американским учёным Данцигом в 1949г., однако, ещё в 1939г. идеи метода были разработаны российским математиком
Л. В. Канторовичем.
Симплексный метод – это итерационный процесс, который начинается с одного решения и в поисках лучшего варианта движется по угловым точкам области возможных решений до тех пор, пока не достигнет оптимального значения, в частности по угловым точкам многоугольника решений, полученного геометрическим методом.
Алгоритм симплексного метода включает следующие этапы:
1. Составление первого опорного плана
2. Проверка плана на оптимальность
3. Определение разрешающих столбца и строки
4. Построение нового опорного плана
Составление первого опорного плана
Если система ограничений задачи дана в виде системы неравенств, правые части которых 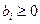 . Перейдем от системы неравенств к системе уравнений путем введения неотрицательных дополнительных переменных. Эти переменные называются базисными. Решим эту систему относительно базисных переменных
. Перейдем от системы неравенств к системе уравнений путем введения неотрицательных дополнительных переменных. Эти переменные называются базисными. Решим эту систему относительно базисных переменных
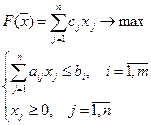
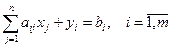 , где
, где 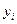 - базисные переменные,
- базисные переменные, 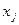 - свободные переменные
- свободные переменные
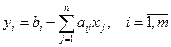
Полагая, что основные переменные 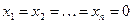 , получим первый опорный план
, получим первый опорный план 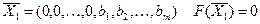 , который заносим в таблицу.
, который заносим в таблицу.
| Б.П. | З.Б.П.(С.Ч.) | 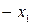 | 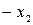 | … | 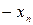 |
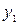 | 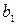 | 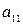 |  | … | 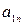 |
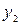 | 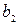 | 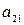 | 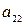 | … | 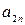 |
| … | … | … | … | … | … |
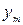 | 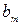 | 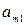 | 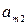 | … | 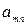 |
| F | 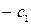 | 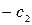 | … | 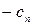 |
Б.П. - базисные переменные, З.Б.П.- значения базисных переменных, С.Ч.- свободные члены, последняя строка таблицы – индексная строка (строка целевой функции).
После составления таблицы просматриваем элементы столбца свободных членов. Если все они положительны, то опорное решение найдено и начинается процесс нахождения оптимального решения.
Алгоритм нахождения оптимального плана
1. Считаем, что в симплексной таблице получено опорное решение. Просматриваем коэффициенты индексной строки. Если все они неотрицательны, то оптимальное решение получено. В этом решении все небазисные переменные равны 0, а базисные переменные равны значению столбца свободных членов.
2. Если среди коэффициентов строки функции (индексной) имеются отрицательные (за исключением свободного члена), то выбираем среди них наибольший по абсолютной величине, и столбец, в котором находится этот коэффициент, берём за разрешающий. Разрешающий столбец показывает, какая переменная на следующей итерации перейдёт из свободных в базисные.
3. Затем элементы столбца свободных членов делим на элементы того же знака (+/+, -/-) разрешающего столбца. Результаты, которые будут всегда положительные, заносим в отдельный столбец симплексных отношений (СО). (Если знаки разные или деление на 0 — в столбце СО прочерк)
4. Разрешающую строку находим по наименьшему симплексному отношению.
5. Элемент таблицы, находящийся на пересечении разрешающих столбца и строки, называют разрешающим и выделяют.
6. С найденным разрешающим элементом рассчитывают новую таблицу;
Правила расчёта элементов новой таблицы:
а) вместо разрешающего элемента в новой таблице ставится обратная ему величина;
б) элементы разрешающей строки делятся на разрешающий элемент;
в) элементы разрешающего столбца делятся на разрешающий элемент и записываются с противоположным знаком;
г) все прочие элементы таблицы вычисляются по формуле, которая носит название прямоугольника:
 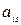 | … | 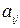 →? →? |
| … | … | … |
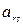 | … | 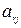 |
Сначала по этому правилу вычисляется произведение элементов 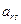 и
и  . Затем произведение элементов расположенных в двух других вершинах прямоугольника. Разность между найденными произведениями делится на разрешающий элемент.
. Затем произведение элементов расположенных в двух других вершинах прямоугольника. Разность между найденными произведениями делится на разрешающий элемент.
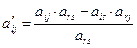 ;
;
После этого анализ новой таблицы начинается с пункта 1, и так до тех пор, пока не найдем оптимального решения или не убедимся, что его не существует.
7. Если в разрешающем столбце таблицы все элементы неположительны, то разрешающую строку выбрать невозможно. Задача в этом случае решения не имеет. Функция в области допустимых решений задачи не ограничена.
8. Если в строке функции в таблице с оптимальным решением имеется хотя бы один нулевой элемент, то задача имеет множество оптимальных решений (есть альтернативные оптимумы).
Пример. Найти максимум функции
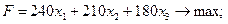
при ограничениях:
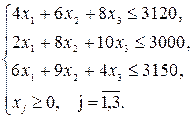
 2014-02-02
2014-02-02 4730
4730
