Приведем систему к каноническому виду:
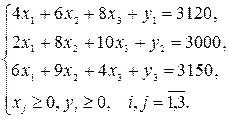
Выразим базисные неизвестные:
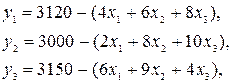
Приравняем свободные переменные к нулю, получим первый опорный план: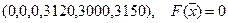 , который заносим в таблицу.
, который заносим в таблицу.
| Б.П. | З.Б.П. | 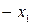 | 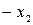 | 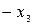 | CO |
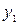 | |||||
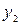 |  2 2 |  1500 1500 | |||
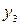 | |||||
| F | -240 | -210 | -180 |
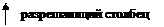
Решение опорное, так как базисные неизвестные принимают положительные значения.
Т.к. в строке функции не все значения положительные, то решение не оптимальное. Переходим к поиску оптимального решения. В строке функции наибольший по абсолютной величине (среди отрицательных) элемент находится в первом столбце, поэтому этот столбец берем за разрешающий. Разрешающую строку находим по наименьшему симплексному отношению. Выделим в таблице разрешающий элемент, который находится на пересечении разрешающих строки и столбца. Рассчитаем элементы новой симплексной таблицы.
| Б.П. | З.Б.П. | 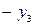 | 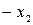 |  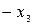 |  CO CO |
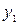 | -2/3 | 16/3 | 191,25 | ||
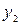 | -1/3 | 26/3 | |||
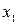 | 1/6 | 3/2 | 2/3 | 787,5 | |
| F |  -20 -20 |
Решение опорное, но не оптимальное.
| Б.П. | З.Б.П. | 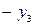 | 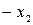 | 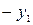 |
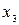 | 191,25 | |||
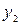 | 292,5 | |||
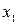 | 397,5 | |||
| F | 37,5 | 3,75 |
Решение оптимальное.
Ответ: 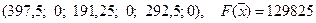
Если необходимо решить задачу, в которой целевая функция идёт на минимум, возможны два способа:
1) для решения задачи достаточно умножить на (-1) функцию F и найти максимум функции –F, т.к. minF = - max (-F);
2) при решении задачи на минимум целевой функции признаком оптимальности плана является отрицательные значения всех коэффициентов индексной строки.
Алгоритм нахождения опорного решения
1. Если среди элементов столбца свободных членов имеются отрицательные, то выбираем любой из них и, просматривая элементы строки с выбранным отрицательным свободным членом, фиксируем в ней отрицательные элементы. Любой столбец с отрицательным элементом в рассматриваемой строке можно брать за разрешающий.
Если же в строке с отрицательным свободным членом нет отрицательных элементов, то система ограничений несовместна. Задача решений не имеет.
2. Разрешающую строку находим по наименьшему симплексному отношению.
3. С выделенным разрешающим элементом, находящимся на пересечении разрешающих строки и столбца, рассчитываем новую симплексную таблицу.
Анализ новой таблицы начинаем с проверки — является ли решение опорным. Так до тех пор, пока не найдем опорное решение, или не убедимся, что его не существует.
Пример:
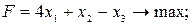
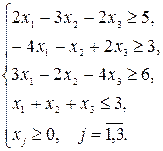
 2014-02-02
2014-02-02 1612
1612








