Чтобы вид системы ограничений был упорядоченным, надо умножить первые 3 ограничения на -1.
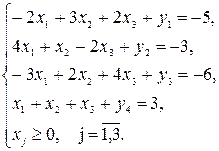
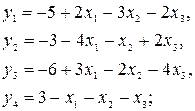
| БП | СЧ |  |  | 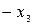 | CO |
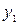 | -5 | -2 | 5/2 | ||
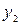 | -3 |  4 4 | -2 | - | |
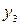 | -6 | -3 |  2 2 | ||
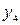 | |||||
| F | 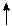 -4 -4 | -1 |
| БП | СЧ | 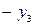 | 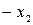 | 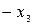 |
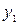 | -1 | -2/3 | 5/3 | -2/3 |
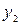 | -11 | 4/3 | 11/3 | 10/3 |
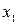 | -1/3 | -2/3 | -4/3 | |
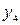 | 1/3 | 5/3 | 7/3 | |
| F | -4/3 | -11/3 | -13/3 |
Ответ: система ограничений несовместна и задача не имеет решения.
Вырожденные задачи линейной оптимизации
Если среди базисных неизвестных в исходной задаче имеется одна или несколько неизвестных равных нулю, или нулевое значение базисной переменной получено на каком-то шаге решения, то имеем вырожденную задачу линейной оптимизации.
Вырожденность может иметь место при нахождении опорного решения и оптимального. Способы ликвидации вырожденности в обоих случаях одни и те же.
Опасность вырожденности.
Если мы находим опорное решение, то в соответствии с алгоритмом за разрешающий столбец принимаем тот, который содержит отрицательный элемент в строке с отрицательным свободным членом. Разрешающей строкой в этом случае будет та, в которой базисная неизвестная равна нулю, т.к. наименьшее симплексное отношение будет равно нулю. Это значит, что величина новой переменной, вводимой в базис, будет равна нулю, и решение в новой таблице останется неопорным. При продолжении процесса, строка с нулевым элементом будет оставаться разрешающей, а изменения будут происходить в наборе базисных и небазисных неизвестных, и мы можем прийти к таблице, которая уже была, т.е. может наступить случай зацикливания.
Чтобы избежать вырожденности, а следовательно, и зацикливания, искусственно припишем нулевому элементу в столбце свободных членов знак ‘+’, а разрешающим столбцом будем выбирать тот, в котором находятся два отрицательных элемента: один – в строке с отрицательным, а другой – в строке с нулевым свободным членом.
Аналогично поступаем с вырожденной задачей при нахождении оптимального решения. За разрешающий столбец выбирается столбец, который содержит два отрицательных элемента: один – в строке с нулевым свободным членом, второй — в строке функции. Разрешающая строка находится, как обычно, по минимальному симплексному отношению.
Если при нахождении опорного или оптимального решения нельзя выбрать разрешающий столбец, в котором были бы два отрицательных элемента, то разрешающий столбец находится по общим правилам.
 2014-02-02
2014-02-02 1285
1285








