Решение.
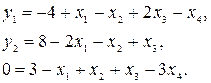
| БП | СЧ | 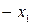 | 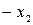 | 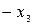 | 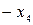 | CO |
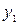 | -4 | -1 | -2 | |||
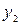 |  2 2 | -1 | ||||
| -1 | -1 |  3 3 | ||||
| -F |
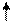
| БП | СЧ | 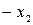 | 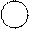 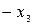 | 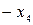 | CO | |
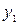 | -1 | -3 |  1/3 1/3 | |||
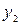 | -2 | -6 | ||||
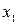 | -1 | -1 | - | |||
| -F | -6 | -2 | -2 |
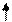
| БП | СЧ | 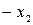 | 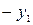 | 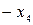 |
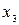 | 1/3 | |||
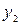 | 5/3 | |||
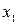 | 10/3 | |||
| -F | -7 |
Ответ: 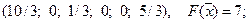
Среди практических задач важное место занимают задачи математического программирования с требованием целочисленности переменных (всех или части).
Решение общей целочисленной задачи является очень сложным. Наиболее разработанными и универсальными являются методы решения задач линейного целочисленного программирования, которые формулируются следующим образом: найти значения неизвестных 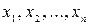 , доставляющих экстремум функции
, доставляющих экстремум функции
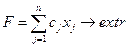
и удовлетворяющих условиям
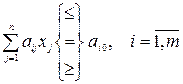 ,
,
а также условиям неотрицательности
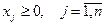
и целочисленности
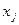 - целые,
- целые, 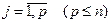 .
.
Метод отсечений (метод Гомори)
Метод Гомори основан на применении симплекс-метода и метода отсечения.
Алгоритм метода
1. Сформулированная задача решается симплекс-методом без учета целочисленности.
2. Если в результате получено целочисленное оптимальное решение, то цель достигнута. В противном случае выбирается переменная с нецелочисленным оптимальным значением (если дробных переменных несколько, то выбирается та, у которой дробная часть больше).
3. Для выбранной неизвестной записывается условие отсечения её нецелочисленного значения в виде линейного неравенства. Новое ограничение добавляется в симплексную таблицу с оптимальным решением, и переходим к шагу 1.
Признаком отсутствия целочисленного решения является отсутствие дробных значений коэффициентов в строке с дробным значением базисной переменной.
Для того чтобы сформулировать правило построения условия отсечения, введем некоторые обозначения. Пусть а есть некоторое действительное число. Обозначим через [ а ]целую часть числа а.
Целой частью числа а называется наибольшее целое число, меньшее или равное а. Приведем примеры нахождения целой части различных чисел:
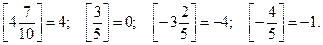
Обратите внимание, что если целая часть положительного числа получается простым отбрасыванием его дробной части, то целая часть отрицательного числа получается отбрасыванием дробной части числа и увеличением модуля полученного результата на единицу.
Обозначим далее через {а} дробную часть числа а. Дробная часть числа а есть разность между данным числом и его целой частью:
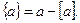
Для чисел, рассмотренных выше, найдем дробные части:
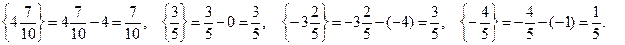
Дробная часть числа всегда положительна.
Чтобы сформулировать условие отсечения в процессе решения задачи целочисленного линейного программирования, необходимо из последней (оптимальной) симплекс-таблицы выписать уравнение, содержащее выбранную нецелочисленную неизвестную хк:
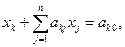
где 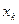 — базисная неизвестная;
— базисная неизвестная; 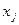 — свободная неизвестная;
— свободная неизвестная; 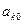 - нецелочисленное значение базисной переменной. Тогда условие отсечения будет иметь вид
- нецелочисленное значение базисной переменной. Тогда условие отсечения будет иметь вид
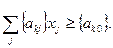
Здесь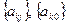 — дробные части соответствующих чисел.
— дробные части соответствующих чисел.
Рассмотрим применение метода отсечений на конкретном примере.
 2014-02-02
2014-02-02 1309
1309
