Пример.
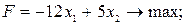
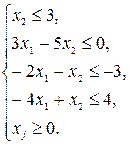
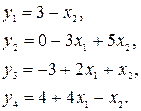
| БП | СЧ | 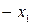 | 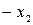 | CO |
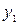 | ||||
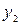 | 0+ | -5 | - | |
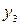 | -3 | -2 |  -1 -1 |  3 3 |
 | -4 | |||
| F | -5 |
| БП | СЧ | 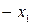 | 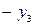 | CO |
 | -2 |  1 1 |  0 0 | |
 | -5 | - | ||
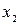 | 3 | -1 | - | |
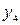 | -6 | |||
| F | -5 |
Опорное решение. Т.к. нельзя выбрать разрешающий столбец с двумя отрицательными элементами, то работаем по общим правилам.
| БП | СЧ | 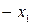 | 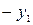 |
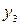 | -2 | ||
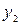 | |||
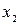 | 3 | ||
 | -4 | -1 | |
| F |
Решение опорное и оптимальное.
Ответ: 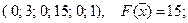
Решение общей задачи линейного программирования
Пусть в задаче линейной оптимизации k ограничений заданы в виде неравенств и m-k ограничений в виде равенств. После приведения ограничений к каноническому виду и разрешения относительно базисных неизвестных в ограничениях-неравенствах слева будут базисные неизвестные, а в равенствах – нули.
Переместим нули в верхнюю строку таблицы. Разрешающим выберем столбец, в котором находится положительный элемент на пересечении со строкой с нулевым элементом. Строка целевой функции на выбор разрешающего столбца на данном этапе влияния не оказывает.
В ходе преобразований столбцы под “переброшенными” наверх нулями можно вычеркивать. Подлежат вычеркиванию и строки, состоящие из одних нулей.
Если в процессе преобразований встретится 0-строка, все элементы которой — нули, а свободный член отличен от нуля, то система ограничительных уравнений решений не имеет.
Если ли же встретится 0-строка, в которой кроме свободного члена других положительных элементов нет, то система не имеет неотрицательных решений.
Пример. Найти минимум целевой функции:
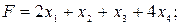
при следующих ограничениях:
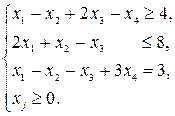
 2014-02-02
2014-02-02 997
997








