Существует несколько методов получения МНКФ функций, использующих понятие простой импликанты, понятия вхождения и накрытия функций, сокращенных и минимальных КНФ аналогично соответствующим понятиям для дизъюнктивных нормальных форм.
Рассмотрим наиболее простой алгоритм поиска МКНФ, использующий выражение МКНФ через инверсию от МКНФ обратной функции.
Обратной функцией f1(x1 x2 … xn) называется
 f2(x1 x2 … xn)= f1(x1 x2 … xn).
f2(x1 x2 … xn)= f1(x1 x2 … xn).
Алгоритм метода.
1) исходную функцию представляют в СДНФ;
2) находят СДНФ обратной функции;
3) пользуясь любым из известных методов, находят МДНФ обратной функции;
4) инверсия от МДНФ обратной функции после соответствующих преобразований с использованием формул де Моргана представляет МКНФ исходной функции.
Пример. Найти МКНФ функции: 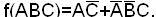
1) СДНФ 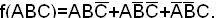
2) Так как обратная функция  имеет значение 1 на тех наборах, на которых f(ABC) принимает значение 0, то в СДНФ обратной функции входят те минтермы, которые отсутствуют в СДНФ функции f(ABC):
имеет значение 1 на тех наборах, на которых f(ABC) принимает значение 0, то в СДНФ обратной функции входят те минтермы, которые отсутствуют в СДНФ функции f(ABC):
СДНФ 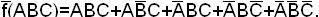
3) Используем метод карт Вейча для отыскания МДНФ обратной функции (рис.9). Сокращенная ДНФ  включает простые импликанты: AC,
включает простые импликанты: AC, 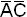 , BC,
, BC, 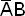 .
.
Из них обязательными является АС и 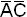 . Функция имеет две минимальные формы:
. Функция имеет две минимальные формы:

4) Переходим к МКНФ f(ABC):
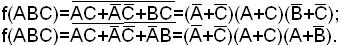
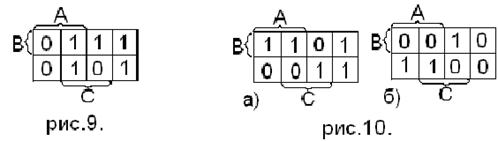
Пример. Найти МКНФ функции:
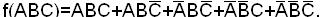
1) Карта Вейча для f(ABC) приведена на рис.10, а.
2) Используем карту Вейча для отыскания МДНФ  (рис.10,б).
(рис.10,б).
Функция  имеет единственную МДНФ:
имеет единственную МДНФ:

3) Находим МКНФ исходной функции:
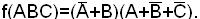
 2014-02-02
2014-02-02 2040
2040
