2014-02-02
1183
Конечной целью анализа САР является решение (если это возможно) или исследование дифференциального уравнения системы в целом. Обычно известны уравнения отдельных звеньев, входящих в состав САР, и возникает промежуточная задача получения дифференциального уравнения системы по известным ДУ её звеньев. При классической форме представления ДУ эта задача сопряжена со значительными трудностями. Использование понятия передаточной функции существенно упрощает её.
Пусть некоторая система описывается ДУ вида
.
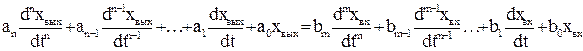Введя обозначение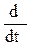 
=p, где pназывают оператором, или символом, дифференцирования, и обращаясь теперь с этим символом как с обычным алгебраическим числом, после вынесения xвых и xвх за скобки, получают дифференциальное уравнение этой системы в операторной форме:
| (anpn +an-1pn-1 +…+a1p +a0)xвых = (bmpm +bm-1pm-1 +…+b1p+b0)xвх. | (4.1) |
Многочлен от p, стоящий при выходной величине,
| D(p)=anpn+an-1pn-1+…+a1p+a0 | (4.2) |
называется собственным оператором, а многочлен при входной величине – оператором воздействия
|
|
|
| K(p) = bmpm +bm-1pm-1 +…+b1p+b0. | (4.3) |
Передаточной функцией называется отношение оператора воздействия к собственному оператору:
| W(p) = K(p)/D(p) = xвых/xвх. | (4.4) |
В дальнейшем мы будем практически всюду использовать именно операторную форму записи дифференциальных уравнений.
Виды соединений звеньев и алгебра передаточных функций.
Получение передаточной функции САР требует знания правил нахождения передаточных функций групп звеньев, в которых звенья соединены между собой определенным образом. Имеется три типа соединений.
1. Последовательное, при котором выход предыдущего звена является входом для последующего (рис. 4.1):
 |
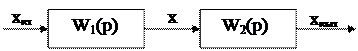Рис. 4.1 Последовательное соединение звеньев
Как видно из уравнения (4.4), передаточная функция любой системы с одной стороны, - это отношение оператора воздействия к собственному оператору, а с другой – это отношение выходной величины ко входной. В данном случае передаточная функция соединения имеет вид
| Wc(p) = xвых/xвх = (xвых/x)(x/xвх) =W1(p)W2(p). | (4.5) |
2. Параллельное, при котором несколько звеньев имеют общий вход, а выходные величины этих звеньев складываются (рис. 4.2):
 |
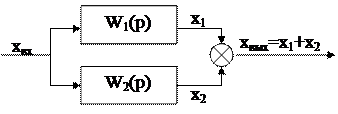Рис. 4.2 Параллельное соединение звеньев
Новый значок на этой схеме – сумматор. Если встречается сумматор с закрашенным сектором, это означает, что величина, входящая в этот сектор, изменяет свой знак.
Как и ранее, базируясь на понятии передаточной функции, получаем:
| Wс(p) = xвых/xвх =x1/x + x2/x =W1(p) + W2(p). | (4.6) |
3. Встречно - параллельное соединение, или охват звена обратной связью (рис. 4.3).
 |
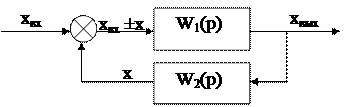Рис. 4.3 Встречно – параллельное соединение.
|
|
|
В зависимости от того, складывается сигнал обратной связи х с входным сигналом хвх либо вычитается из него, различают положительные и отрицательные обратные связи.
Попрежнему базируясь на свойстве передаточной функции, можем написать
| W1(p) =xвых/(xвх±х); W2(p) = x/xвых; Wc =xвых/xвх. | (4.7) |
Исключив из первых двух уравнений внутреннюю координату х, получим передаточную функцию для такого соединения:
| Wc(p) = W1(p)/[1±W1(p)W2(p)]. | (4.8) |
Следует иметь в виду, что в последнем выражении знак плюс соответствует отрицательной обратной связи.
В том случае, когда какое-нибудь звено имеет несколько входов (как, например, объект регулирования), рассматриваются несколько передаточных функций этого звена, соответствующие каждому из входов, например, если уравнение звена имеет вид
| D(p)y = Kx(p)x + Kz(p)z, | (4.9) |
где Kx(p) и Kz(p) – операторы воздействий соответственно по входам x и z, то это звено имеет передаточные функции по входам х и z:
| Wx(p) = Kx(p)/D(p); Wz(p) = Kz(p)/D(p). | (4.10) |
В дальнейшем в целях сокращения записей в выражениях передаточных функций и соответствующих операторов будем опускать аргумент «p».
Из совместного рассмотрения выражений (4.9) и (4.10) следует, что
| y = Wxx+Wzz, | (4.11) |
то есть в общем случае выходная величина любого звена с несколькими входами равна сумме произведений входных величин на передаточные функции по соответствующим входам.
Передаточная функция САР по возмущению.
Обычный вид структуры САР, работающей по отклонению регулируемой величины, таков:
 |
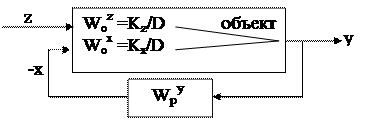Рис. 4.4 Замкнутая САР
Обратим внимание на то обстоятельство, что регулирующее воздействие поступает на объект с измененным знаком. Связь между выходом объекта и его входом через регулятор называется главной обратной связью (в отличие от возможных дополнительных обратных связей в самом регуляторе). По самому философскому смыслу регулирования действие регулятора направлено на уменьшениеотклонения регулируемой величины, и потому главная обратная связь всегда отрицательна. На рис. 4.4:
Woz - передаточная функция объекта по возмущению;
Wox- передаточная функция объекта по регулирующему воздействию;
Wpy - передаточная функция регулятора по отклонению у.
Дифференциальные уравнения объекта и регулятора выглядят так:
 |
y=Woxx +Wozz
x = - Wpуy. (4.12)
Подставив х из второго уравнения в первое и выполнив группировку, получаем уравнение САР:
| (1+WoxWpу)y = Wozz. | (4.13) |
Отсюда передаточная функция САР по возмущению
| Wcz= y/z =Woz/(1+WoxWpу). | (4.14) |
Подобным путём можно получить и передаточную функцию САР по управляющему воздействию:
| Wcu = WoxWpu/(1+WoxWpy), | (4.15) |
где Wpu -передаточная функция регулятора по управляющему воздействию.
