B 0 0 1 1 0 0 1 1
 C 0 1 0 1 0 1 0 1
C 0 1 0 1 0 1 0 1
f(ABC) 1 0 0 0 - 1 1 -
МДНФ 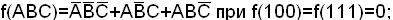
МДНФ 
Рассмотрим общий метод получения МДНФ не полностью определенных булевых функций.
Пусть булева функция f(x1 x2 … xn) не определена на p наборах аргументов. Тогда полностью определенная функция φ(x1 x2 … xn) называется эквивалентной функции f(x1 x2 … xn), если ее значения совпадают со значениями функции f(x1x2…xn) на тех наборах, на которых последняя определена.
Если функция f(x1 x2 … xn) не определена на р наборах, то существует 2p различных функций, эквивалентных данной.
Задача минимизации не полностью определенных функций сводится к отысканию такой эквивалентной функции φi(x1x2…xn), которая имеет простейшую минимальную форму.
Введем эквивалентные функции φ0(x1x2…xn) и φ1(x1x2…xn), которые на всех запрошенных наборах функции f(x1x2…xn) принимают значения 0 и 1 соответственно.
Теорема. Минимальная ДНФ не полностью определенной функции f(x1x2…xn) совпадает с дизъюнкцией тех самых коротких импликант функции φ1(x1x2…xn), которые совместно поглощают все единицы функции φ0(x1x2…xn) и ни одна из них не является лишней.
Доказательство следующее.
Предположим, что φi(x1x2…xn) – некоторая эквивалентная функция. Тогда все минтермы СДНФ φi входят в СДНФ функции φ1. Поэтому любая импликанта функции φi(x1x2…xn) будет совпадать с импликантой функции φ1 или поглощаться ею, т.е. среди импликант функции φ1 всегда найдется такая, которая поглощает любую импликанту любой эквивалентной функции φ1. Следовательно, самыми короткими импликантами из всех накрывающих единицы функции f(x1x2…xn) будут импликанты функции φ1.
Среди всех эквивалентных функций φ0 имеет минимальное количество минтермов. Следовательно, и количество простых импликант (из набора импликант функции φ1), необходимых для поглощения минтермов φ0, будет минимальным. Дизъюнкция самых коротких импликант функции φ1, которые совместно накрывают все единицы φ0, представляет МДНФ f(x1x2…xn).
Пример. Найти МДНФ функции:
 причем наборы <
причем наборы <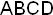 >, <
>, <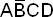 >, <
>, < 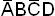 >, <
>, < 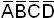 > являются запрещенными.
> являются запрещенными.
Проводим процедуру, описанную в методе Квайна, используя минтермы как функциональных, так и запрещенных наборов функции:

Составляем импликантную матрицу (табл.21), используя минтермы только функциональных наборов функции.
Таблица 21
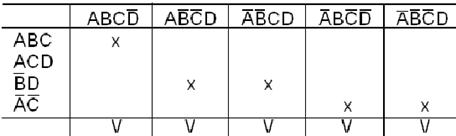
Минимальная форма исходной функции
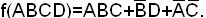
Импликанта ACD не поглощает ни один минтерм функциональных наборов, так как образована из тех минтермов функции φ1, которые в φ0 не входят.
Пример. Найти МДНФ и МКНФ не полностью определенной функции 
Причем наборы 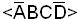 ,
,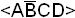 и
и 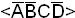 являются запрещенными.
являются запрещенными.
Используем метод карт Вейча (рис.11).
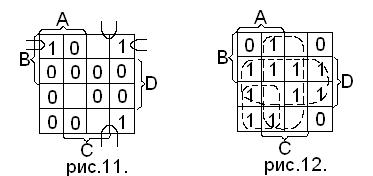
Незаполненные клетки карты соответствуют запрещенным наборам.
Карта для обратной функции 
 приведена на рис.12.
приведена на рис.12.
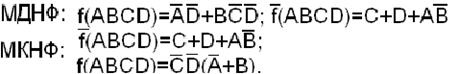
До сих пор мы рассматривали проблему минимизации функций, относящихся к классу ДНФ. Однако очень часто МДНФ функции можно упростить введением скобочной записи.
Пример. f(ABCD)=m8+ m9+ m10+ m11+ m14+ m15;
МДНФ 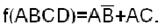
Однако более простая запись получится при вынесении А за скобки:
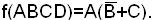
Поэтому возникла проблема нахождения абсолютных минимальных представлений для булевых функций.
Определение. Выражение Q называется абсолютным минимальным представлением для функции f(x1x2…xn), если в базисе {/\,\/,ˉ} не существует более минимальных представлений, каким бы способом ни получалось это выражение.
Встает вопрос: не является ли абсолютными минимальными выражения, которые могут быть получены их МКНФ путем всевозможных вынесений за скобки и выбором наиболее простого выражения из этих скобочных форм.
Беркхарт показал, что существуют такие минимальные выражения, которые не могут быть получены при вынесении за скобки в МДНФ или МКНФ.
В работах Абхъянкара дан алгоритм непосредственного нахождения абсолютных минимальных выражений для данной функции. Однако этот алгоритм практически неприменим даже при малом n из-за большого количества необходимых операций.
Так, на последнем этапе получения абсолютного минимального выражения функции n переменных число операций оценивается как
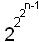 +1≤m≤
+1≤m≤ 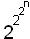 .
.
При n=4 2257≤m≤265536.
Таким образом, нахождение абсолютных минимальных выражений функции с числом переменных больше четырех по имеющемуся алгоритму Абхъянкара становится неприемлимым даже при использовании средств вычислительной техники.
Более практической является минимизация МДНФ путем вынесения за скобки.
 2014-02-02
2014-02-02 1662
1662
