Синтез логических схем на интегральных элементах.
Раздел 3.
Рассмотрим схемы элементов, реализующих функцию стрелка Пирса «↓» (элемент «ИЛИ-НЕ») и функцию Шеффера «|» (элемент «И-НЕ») (рис.42).
Основные соотношения в системах { ↓ } и { | }:
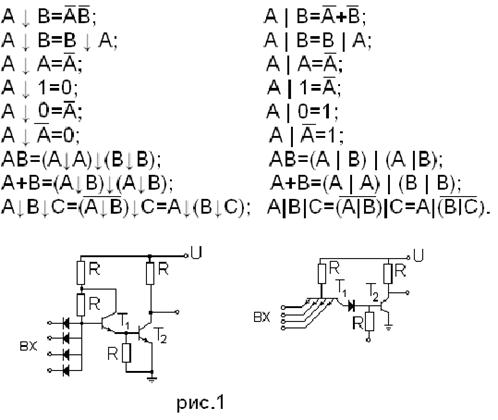
Функции Шеффера и Пирса связаны соотношениями, аналогичными формулам де Моргана:

1. Функция задана в ДНФ:
f(x1 x2… xn)=K1+ K2+…+ Km,
здесь Km – элементарные произведения.
Берем двойное отрицание выражения, используем теорему де Моргана и переходим к базису { ↓ }:
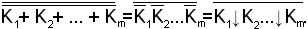
Рассмотрим элементарное произведение
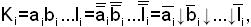
где ai =x1 или 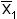 ; bi =x2 или
; bi =x2 или  и т.д.
и т.д.
Такую процедуру следует провести над каждым элементарным произведением, тогда
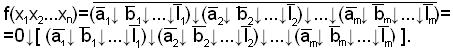
Таким образом, чтобы перейти от ДНФ к функции Пирса, необходимо все элементарные произведения заключить в скобки, а затем все знаки дизъюнкции и конъюнкции заменить знаком стрелки Пирса, взять инверсии от всех переменных, заключенных в скобках, и общую инверсию от полученного выражения А записью 0↓А или А↓0. Аналогично все инверсии переменных заменить через выражение 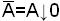 или
или 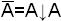 .
.
При этом следует помнить, что любое произведение в сходном выражении должно содержать не менее двух переменных. Это можно получить с помощью соотношения 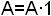 .
.
Пример.
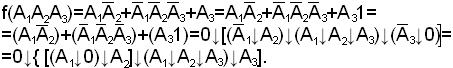
2. Функция задана в КНФ:
f(x1 x2… xn)=Q1+ Q2+…+ Qm,
здесь Qi – элементарные суммы.
 2014-02-02
2014-02-02 877
877








