Непосредственным интегрированием называется вычисление интегралов путем использования таблицы основных неопределенных интегралов, их свойств, а также тождественных преобразований подынтегрального выражения.
Пример 1. Найти 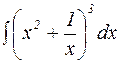 .
.
Решение: 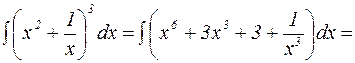
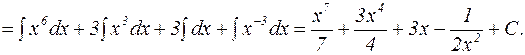
Пример 2. Найти 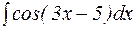 .
.
Решение: Воспользуемся свойством 5:
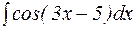 =
= 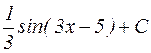 .
.
Пример 3. Найти 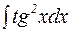 .
.
Решение: Воспользуемся формулами тригонометрии:
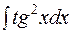 =
= 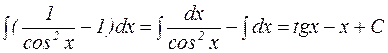 .
.
2. Интегрирование путем подведения под знак дифференциала.
Все формулы таблицы основных интегралов справедливы, когда переменная интегрирования не является независимой, а представляет функцию от некоторой другой переменной: 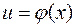 .
.
Тогда 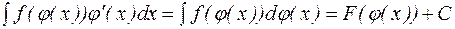
или 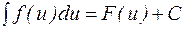 .
.
Пример 4. Вычислить интеграл 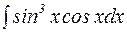 .
.
Решение: Так как 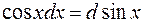 , то
, то
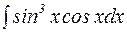 =
= 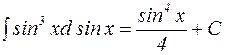 .
.
Здесь мы применили формулу 1 таблицы интегралов.
Пример 5. Вычислить интеграл 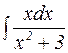 .
.
Решение: Заметим, что 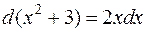 , тогда имеем:
, тогда имеем:
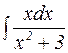 =
= 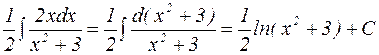 .
.
 2015-02-04
2015-02-04 923
923








