 Предпологаем что ψu=0
Предпологаем что ψu=0
u(t) = Umsinωt
UR(t) 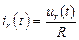
т.к 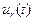 =
=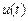
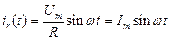
мгновенная мощность рассеиваемая на резистивном элементе равна
iL(t) i(t) = Im sinωt
UL(t) 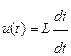

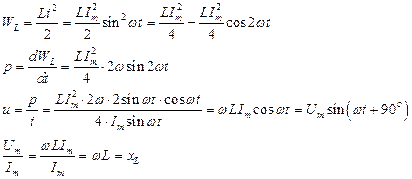 4.3 Емкостной элемент
4.3 Емкостной элемент
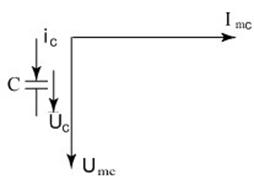
 iС(t) u(t) = Um sinωt
iС(t) u(t) = Um sinωt
UС(t) 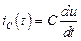
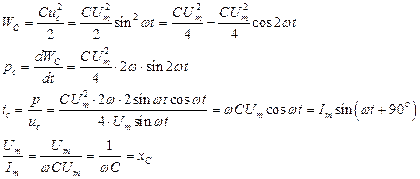 4.4 Анализ последовательной цепи переменного тока
4.4 Анализ последовательной цепи переменного тока
Мы показали, что при заданном токе напряжения на пассивных элементах будут следующими:
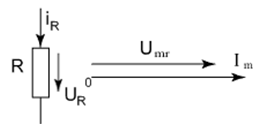
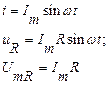
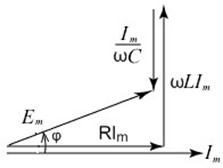
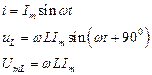
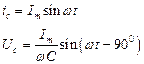
Все рассмотренные элементы объединим в последовательную цепь (рис.4.1) ток в ней известен. Определим параметры мгновенного значения ЭДС.
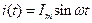
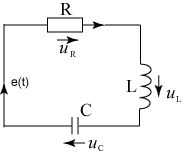
Рис.4.1.
Неизвестная ЭДС также будет иметь вид гармонической функции.
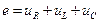
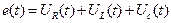
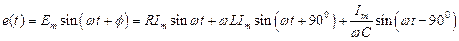
Данное выражение представляет собой уравнение для электрической цепи, записанное по II закону Кирхгофа (для установившегося режима).
Полагая, в частности, ωt = π/2 и ωt = 0, получим RIm = Umcosφ; (ωL – 1/ωC)Im = Umsinφ.
Возведя первое и второе равенства в квадрат и сложив, получим:
[ R2 + (ωL – 1/ωC) ] Im2 = Um2
Откуда находим связь между амплитудами тока и напряжения:
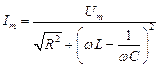
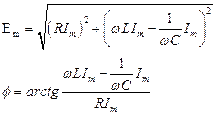

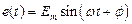
Если в той же последовательной цепи заданной будет ЭДС: e(t) = Emsinωt, то i(t) = Imsin(ωt ± φ).
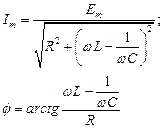
Полученные соотношения можно использовать для расчёта мгновенных значений напряжения и тока в последовательной цепи, питаемой от источника гармонической ЭДС.
Рассмотрим несколько примеров.
 2014-02-02
2014-02-02 1833
1833

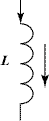
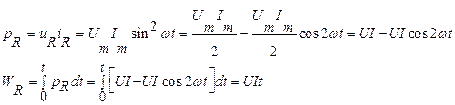 4.2
4.2 






