Зубчатые передачи

Зубчатые передачи обеспечивают передачу момента вращения с помощью последовательно зацепляющихся зубьев. Тела вращения, на которых расположены зубья, называются зубчатыми колесами. Меньшее колесо зубчатой пары называ­ется шестерней, а большее - колесом. Собственно колесо состоит из диска со ступицей и зубчатого венца (рис.З.1.).

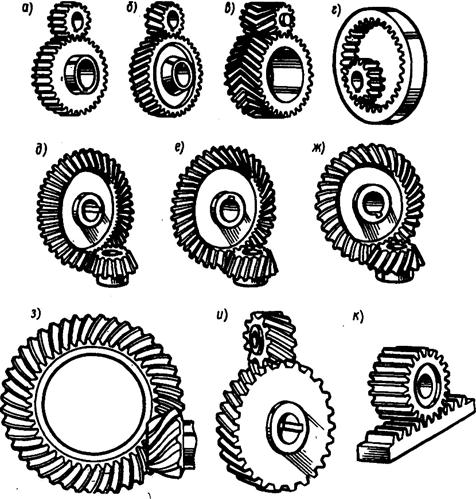
Рис.3.2

Все применяемые здесь и в дальнейшем термины, определения и обозначения, относящиеся к зубчатым передачам, соответствуют ГОСТ 16530—83 «Передачи зубчатые», ГОСТ 16531—83 «Передачи зубчатые цилиндрические» и ГОСТ 19325—73 «Передачи зубчатые конические».

Зубчатое зацепление представляет собой высшую кинематическую пару, так как зубья теоретически соприкасаются между собой по линиям или точ­кам, причем меньшее зубчатое колесо пары называется шестерней, а большее — колесом. Сектор цилиндрического зубчатого колеса бес­конечно большого диаметра называется зубчатой рейкой.

Зубчатые передачи можно классифицировать по многим признакам, а именно: по расположению осей валов (с параллельными, пересекающи­мися, скрещивающимися осями и соосные); по условиям работы (закры­тые — работающие в масляной ванне и открытые — работающие всухую или смазываемые периодически); по числу ступеней (одноступенчатые, многоступенчатые); по взаимному расположению колес (с внешним и внутренним зацеплением); по изменению частоты вращения валов (по­нижающие, повышающие); по форме поверхности, на которой нарезаны зубья (цилиндрические, конические); по окружной скорости колес (тихо­ходные при скорости до 3 м/с); среднескоростные при скорости до 15 м/с, быстроходные при скорости выше 15 м/с); по расположению зубьев отно­сительно образующей колеса (прямозубые, косозубые, шевронные, с кри­волинейными зубьями); по форме профиля зуба (эвольвентные, круговые, циклоидальные). Наиболее распространен эвольвентный профиль зуба, предложенный Эйлером в 1760 г. Он обладает рядом существенных технологических и эксплуатационных преиму­ществ. Круговой профиль зуба предложен М.Л.Новиковым в 1954 г.. По сравнению с эвольвентным он позволяет повысить нагрузку передач.

Кроме перечисленных существуют передачи с гибкими зубчатыми колесами, называемые волновыми.

Основные виды зубчатых передач (рис. З.2. ) с параллельными осями: а — цилиндрическая прямозубая, б — цилиндрическая косозубая, в — шевронная, г — с внутренним зацеплением; с пересекающимися осями', д — коническая прямозубая, е — коническая с тангенциальными зубьями, ж — коническая с криволинейными зубьями; со скрещивающимися осями: з — гипоидная, и — винтовая; к — зубчато-реечная прямозубая.

Зубчатая передача, оси которой расположены под углом 90°, называ­ется ортогональной.

Достоинство зубчатых передач заключается, прежде всего, в том, что при одинаковых характеристиках они значительно более ком­пактны по сравнению с другими видами передач. Кроме того, зубчатые передачи имеют более высокий КПД (до 0,99 в одной ступени), сохраня­ют постоянство передаточного числа, создают относительно небольшую нагрузку на опоры валов, имеют большую долговечность и надежность рабо­ты в широких диапазонах мощностей (до десятков тысяч киловатт), окруж­ных скоростей (до 150 м/с) и передаточных чисел (до нескольких сотен).

Недостатки зубчатых передач: сложность изготовления точных передач, возможность возникновения шума и вибраций при недостаточ­ной точности изготовления и сборки, невозможность бесступенчатого регулирования частоты вращения ведомого вала.

Зубчатые передачи являются наиболее распространенными типами механических передач и находят широкое применение во всех отраслях машиностроения, в частности в металлорежущих станках, автомобилях, тракторах, сельхозмашинах и т. д.; в приборостроении, часовой промыш­ленности и др.

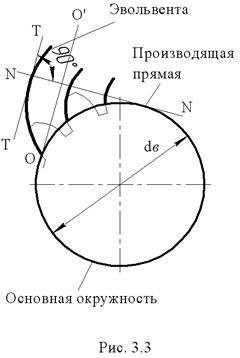
Свойства эвольвентного зацепления. Эвольвентой или разверткой окружности называют плоскую кривую, которая описывается любой точкой прямой NN, перекатываемой без скольжения по неподвиж­ной окружности (рис. 3.3). Линию NN называют производящей прямой, а окружность диаметра d_b, по которой эта прямая перекатывается, — ос­новной окружностью. Так как перекатывание производящей прямой по основной окружности происходит без скольжения, то в каждый данный момент точка их касания является мгновенным центром скоростей и цен­тром кривизны эвольвенты, следовательно, производящая прямая в каждом своем положении будет нор­малью к эвольвенте, иначе говоря, нормаль эвольвенты всегда явля­ется касательной к основной ок­ружности.

Из способа образования эволь­венты следует, что эта кривая не может существовать внутри ос­новной окружности. Если перекаты­вать производящую прямую в про­тивоположном направлении, то по­лучим другую ветвь эвольвенты — левую (эвольвенты, изображенные на рис. 3.3. жирной линией, пра­вые). Каждый зуб колеса с эвольвентным зацеплением очерчивает­ся участками правой и левой эвольвент (рис. 3.3 ); форма зубьев внутри основной окружности опреде­ляется профилем зуборезного инструмента. Две одноименные (правые или левые) эвольвенты эквидистантные (равноудаленные) кривые, т.е. имеющие между собой одинаковое расстояние по любой общей нор­мали, равное длине дуги основной окружности между началом эвольвент. Очевидно, что с увеличением диаметра db основной окружности ра­диусы кривизны эвольвенты будут увеличиваться, а в пределе при d_b → 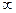эвольвента обращается в прямую, следовательно, у рейки

Рис. 3.4

с эвольвентным зацеплением профиль зубьев должен быть прямолиней­ным. Именно поэтому в основу проектирования цилиндрических и кони­ческих зубчатых

колес эвольвентного зацепления положены стандарт­ные исходные контуры, представляющие собой контур рейки с зубьями прямолинейного профиля (см. рис. 3.11).

Рассмотрим (рис. 3.4) схему эвольвентного зацепления пары зубьев колёс, вращающихся вокруг осей О1 и О₂ с угловой скоростью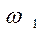и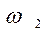

Положение полюса зацепления П определяется согласно основной теоре­ме зацепления, а общая нормаль NN к профилям зубьев в точке контакта — касательная к основным окружностям 1 и 2, диаметры которых в соответ­ствии со стандартом обозначены db1 и d_b2. Так как основные окружности имеют постоянный диаметр, то общая нормаль NN и полюс П будут за­нимать постоянное положение, следовательно, точка контакта зубьев перемещается по общей нормали, называемой поэтому линией зацепле­ния. Прямая линия зацепления присуща только эвольвентному зацеплению.

Угол α между линией зацепления NN и общей касательной ТТ к на­чальным окружностям называется углом зацепления; его стандартное зна­чение для эвольвентного зацепления α = 20°.

Если для той же пары колес немного изменить межосевое расстояние a_w, то изменится угол зацепления а, но диаметры основных окружностей останутся неизменными.

Так как d_bl = d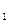c osα, d_b2 = d ₂cosα (рис. 3.4 ), то передаточное от­ношение

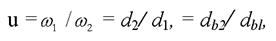(3.1)

Tаким образом, передаточное отношение эвольвентного зацепления зависит только от диаметров основных окружностей, следовательно, из­менение межосевого расстояния не влияет на кинематическую точ­ность эвольвентного зацепления, что является весьма существенным его достоинством.

При изменении межосевого расстояния a_w окружности диаметров d ₁и d₂, перестанут касаться друг друга в полюсе П, т. е. появятся новые на­чальные окружности, которые будут проходить через полюс П и в про­цессе зацепления перекатываться друг по другу без скольжения; поэтому окружности диаметров d ₁и d₂, не зависящие от межосевого расстояния, будем впредь называть делительными. Если межосевое расстояние пере­дачи точно равно полусумме диаметров делительных окружностей, то начальные и делительные окружности совпадают. Таким образом, на­чальная окружность — понятие кинематическое и для отдельно взятого зубчатого колеса не существует. Основные параметры зубчатого колеса определяются по делительной окружности.

Зуб колеса расположен между окружностью вершин зубьев и ок­ружностью впадин. Участок В₁В₂ линии зацепления NN (рис.3.4), заклю­ченный между окружностями вершин зубьев, называется активной лини­ей зацепления. Часть профиля зуба, по которой происходит взаимодейст­вие с зубом парного колеса, называется активным профилем зуба (на рис. 3.4 активные профили заштрихованы).

Угол поворота колеса передачи от положения входа зуба в зацепле­ние до положения выхода из него называется углом перекрытия и обо­
значается 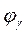(у косозубой передачи угол перекрытия 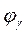состоит из угла
торцового перекрытия 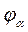(см. рис.3.4)
и угла осевого перекрытия 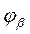). Цен­
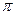тральный угол φ_d (см. рис.3.4), равный 2/z или 360°/z (где z — число зубьев колеса), называется Рис.3.5

угловым шагом. Отношение угла пере­крытия колеса к его угловому шагу называется коэффициентом перекрытия передачи и обозначается е, тогда

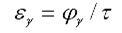(3.2)

Для обеспечения непрерывности зацепления необходимо выполнить условие

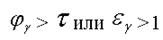(3.3)

иначе пара зубьев выйдет го зацепления раньше, чем войдет в зацепление следующая пара. Таким образом, если 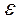< 2, период зацепления одной пары зубьев состоит из периода однопарного и периода дву-парного зацепления. Чем больше коэффициент перекрытия, тем меньше период однопарного зацепления.

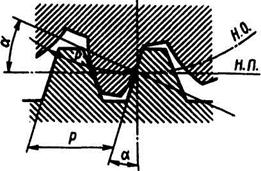
На рис. 3.5 изображено зацепление зубчатого колеса с рейкой, в ко­тором начальная окружность (Н.О.) колеса перекатывается без скольжения по начальной прямой (Н.П.) рейки. Угол профиля зуба рейки и угол зацепления, обозначенные a, равны между собой.