Лекция 2. Модели принятия решений

Для того, чтобы строить модели управления организационными системами необходимо иметь модели поведения людей, входящих в эти системы, то есть, иметь модели принятия людьми решений.

Как описывается поведение человека? В экономике с середины XIX века существует концепция максимизации полезности, то есть концепция экономического человека, который ведет себя таким образом, чтобы максимизировать свою полезность. Несмотря на всю ограниченность этой теории - не всегда понятно, что такое полезность, почему человек стремится ее максимизировать и т.д., - концепция оказалась плодотворной, и ничего лучшего пока не изобретено.

Пусть имеется один субъект (агент), который может выбирать действия из некоторого множества. Предположим, что предпочтения этого субъекта описываются функцией полезности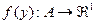 (или целевой функцией, функцией предпочтения - будем использовать эти термины как синонимы), которая отображает множество его действий (альтернатив) A на числовую ось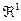. Значения этой функции позволяют сравнивать разные альтернативы. Если взять некоторые два допустимых действия, то лучшим будет то, которое приводит к большему значению функции. Следовательно, агент будет максимизировать свою полезность и производить выбор из множества выбора, которое представляет собой множество максимумов его целевой функции: 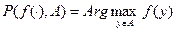. Значит, множество выбора агента зависит от его предпочтений 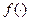и от того множества A, из которого он производит выбор.

Предположение, что агент производит выбор из множества выбора, то есть стремится максимизировать свою целевую функцию, называется гипотезой рационального поведения, которая заключается в том, что агент выбирает с учетом всей имеющейся у него информации наилучшую с его точки зрения допустимую альтернативу, то есть ту альтернативу, на которой достигается максимум его целевой функции.

Описывая модель поведения управляемого субъекта, зная, что управление - некоторое воздействие на него, в рамках этой модели видно, что воздействовать на субъекта можно, влияя на его целевую функцию (мотивационное управление) и влияя на то множество, из которого он делает выбор (институциональное управление).

Пример 2.1. Пусть агент - промышленное предприятие - осуществляет выбор своего действия - объема производимой им продукции 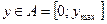, где y _max - максимально возможный при заданных ограничениях (технологических и др.) объем производства. Продукция предприятия продается по цене 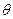>0 за единицу, а производство требует затрат y ² / 2 r, где r >0 - эффективность производства. Целевая функция предприятия (его прибыль) равна разности между доходом от продаж и затратами:

f (y) = 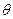y-y²/2r.

Если предприятие стремится производить продукцию в объеме, максимизирующем его прибыль, то оно выберет действие

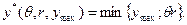
Оптимальное действие предприятия зависит от: рыночной цены 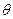, эффективности производства r и технологических ограничений y_max. • (Символ «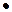.» здесь и далее обозначает окончание примера, доказательства и т.д.)

Приведенная модель принятия решений простая, даже, наверное, слишком простая, и в жизни редко бывает так, что выбор субъекта однозначно определяет его выигрыш - иногда вмешиваются какие-то факторы, которые субъекту, принимающему решения, не подконтрольны. Попробуем учесть их в модели следующим образом: пусть существует неопределенный фактор 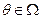- состояние природы. Предпочтения субъекта (агента) зависят от того, что выбирает он сам, и от этого состояния природы, то есть предпочтения определены на декартовом произведении множества допустимых действий и множества возможный состояния природы, а целевая функция отображает это декартово произведение в числовую ось: .

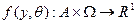Записать такую же простую формулу, как и для предыдущего случая, для такой целевой функции нельзя, потому что, если агент будет выбирать действие, максимизирующее его целевую функцию, то максимум будет зависеть от того, какое значение принимает состояние природы. Для того чтобы описать принятие решений в условиях неопределенности, нужно ввести новую гипотезу - гипотезу детерминизма: субъект, принимая решение, стремится устранить неопределенность и принимать решения в условиях полной информированности. Для этого он должен перейти от целевой функции, зависящей от неопределенных факторов, к целевой функции, которая зависит только от того, что он может выбрать сам.

Здесь возможны следующие варианты:

1) Подстановка какого-то конкретного значения 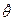состояния природы в целевую функцию и поиск максимума f (y,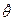) по y. Но не всегда просто ответить на вопрос – а какое конкретное значение 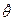надо подставлять.

2) Предположим, что агент – пессимист и считает, что реализуется наихудшее состояние природы. Такой принцип принятия решений называется принципом максимального гарантированного результата и заключается в следующем: действие агента будет доставлять максимум его целевой функции при условии, что он рассчитывает на наихудшее для себя значение неопределенного параметра. Тогда он вычисляет сначала минимум по состоянию природы, а потом максимум по своему действию:

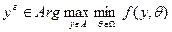
Преимущества данного принципа принятия решений: он дает оценку снизу значения целевой функции (если подставить действие агента в его целевую функцию, то меньше данного значения он не получит), то есть это – точка отсчета снизу. Он плох своей крайней пессимистичностью, так как, если природа не настроена против лица, принимающего решения (ЛПР), то вычисление минимума может дать сильно заниженную оценку.

3) Естественно, можно использовать и другую крайность – крайний оптимизм. То есть, рассчитывать на то, что природа к ЛПР благосклонна, и «выбирает» свое «действие», которое наиболее благоприятно для ЛПР. Тогда следует выбирать максимум целевой функции при условии реализации наилучшего состояния природы:

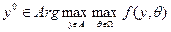
Такой принцип принятия решений называется критерий оптимизма: он дает оценку сверху. Этим он хорош, но этим он и плох. Крайний оптимизм, как и крайний пессимизм, в жизни редко встречаются!

Возможны любые комбинации этих критериев, можно брать их линейную свертку, то есть, балансировать между оптимизмом и пессимизмом.

Предположим теперь, что появилась дополнительная информация о значении неопределенного параметра 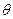, принадлежащего множеству 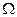. Пусть известно распределение вероятностей p (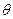) на этом множестве (соответствующая неопределенность называется вероятностной), тогда логично использовать это знание, и устранять неопределенность следующим образом: имеется целевая функция, зависящая от действия агента и значения неопределенного параметра. Взяв математическое ожидание по известному распределению, получим функцию ожидаемой полезности (ожидаемой с точки зрения математического ожидания) .

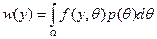Теперь, устранив неопределенность взятием математического ожидания, снова получили детерминированную модель. Можно максимизировать функцию ожидаемой полезности, зависящей только от действия, выбором этого действия.

Пример 2.1. Предположим, что в условиях примера 2.1 ограничения на объем производства отсутствуют 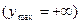, а относительно будущего значения рыночной цены имеется неопределенность: 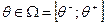. Обозначим 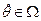- значение цены продукции предприятия, которое сложится на момент продажи.

В соответствии с принципом максимального гарантированного результата предприятие должно ориентироваться на цену 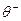(так как именно это значение минимизирует его целевую функцию f (y) = 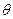y-y²/2r). Выбирая действие 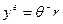, предприятие получит прибыль .

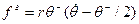Действуя в соответствии с критерием оптимизма, предприятие будет рассчитывать на максимальную цену, выберет действие 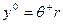и получит прибыль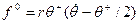

Если бы предприятию априори была известна рыночная цена 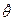, то есть если бы неопределенность отсутствовала, то оно бы выбрало действие и получило бы прибыль .

Если бы имела место вероятностная неопределенность - предприятию было бы, например, известно, что цена равномерно распределена на отрезке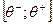, то, вычисляя математическое ожидание 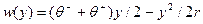, оно выбрало бы действие 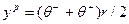и получило бы прибыль

.

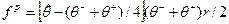Видно, что наличие неопределенности приводит к снижению прибыли предприятия по сравнению со случаем полной его информированности. Например, пусть r =1, 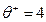,,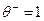 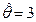. Тогда

; ; ;.

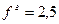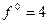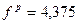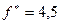Возможны и другие способы устранения неопределенности. Можно рассчитать риск - например, вероятность того, что значение целевой функции окажется меньше, чем заданное. И этот риск минимизировать, то есть использовать не первый момент распределения, а дисперсию и другие характеристики. Подходы могут быть разные, главное - устранить зависимость от неопределенного параметра, что необходимо в силу гипотезы детерминизма, которая требует, чтобы неопределенность была устранена (с учетом всей имеющейся информации!), а потом решения принимались в условиях полной информированности.

Возможна другая информация - могут быть известны значения функций принадлежности для состояний природы (нечеткая неопределенность).

Будем усложнять ситуацию дальше. Мы начали с того, что была функция, зависящая только от действия агента, потом добавили неопределенность в виде параметра, описывающего внешнюю среду. Но агент взаимодействует с другими агентами, а значит, необходимо уметь описать это взаимодействие. Такими описаниями занимается теория игр.