Элементы теории игр

Теория игр описывает игру - такое взаимодействие субъектов, что выигрыш каждого из них в общем случае зависит от действий всех.

Формализуем эту ситуацию. Пусть задано множество игроков N = {1,2,..., n }. i -ый игрок выбирает действие y_i из множества своих допустимых действий , 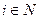. Действия всех игроков называются ситуацией игры: y = (y₁,...,y_n). Целевая функция i -го игрока зависит от вектора действий всех игроков y и является отображением 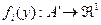множества, являющегося декартовым произведением множества допустимых действий всех игроков 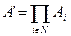, в числовую ось. То есть каждой ситуации – комбинации действий игроков - соответствует некоторый выигрыш каждого из них. Совокупность 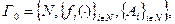множества игроков (агентов), целевых функций и допустимых множеств действий агентов называется игрой в нормальной форме при условии, что каждый из игроков выбирает свои действия однократно, одновременно с другими игроками и независимо (не имея возможности договариваться с ними о своих стратегиях поведения) - модель некооперативного поведения.

Рассмотрим целевую функцию i -го игрока и попробуем применить к ней гипотезу рационального поведения. Игрок рационален, i- ый игрок выбирает i -ую компоненту вектора y, и своим выбором пытается максимизировать свою целевую функцию: 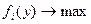. Но то его действие, на котором достигается максимум его целевой функции, будет зависеть от выбора других агентов. Задача такого вида в некотором смысле бессмысленна, так как ее решением будет действие 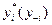, зависящее от действий всех других игроков - его оппонентов - вектора y_-i = (y₁,...,y_i-1,y_i+1,...,y_n), который называется обстановкой игры для i -го игрока (агента).

Для того чтобы выбрать свое действие, агенту нужно знать, как будут себя вести остальные. Значит, нужно делать предположения о поведении остальных игроков. По аналогии с тем, как устранялась неопределенность в случае, когда решения принимал один субъект, здесь имеется множество игроков с так называемой игровой неопределенностью, то есть неопределенностью, порождаемой целенаправленным поведением других игроков. Каждый игрок не всегда может априори точно сказать, что сделают остальные. Рассмотрим возможные варианты.

1) Пусть i -ый игрок считает, что все остальные игроки играют против него. Это - критерий пессимизма, который соответствует тому, что есть i -ый игрок выбирает действие , где 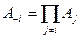. Он считает, что остальные игроки, несмотря на свои собственные интересы, будут действовать против него, а уж выбором своего действия он будет максимизировать то, что зависит от него самого. Плох такой принцип принятия решений тем, что игрок забывает про то, что у остальных есть свои интересы, и, наверное, цель каждого игрока - максимизировать свою целевую функцию, а не «напакостить» оппоненту (это может быть частным случаем целевой функции, но, к счастью, не всегда в жизни так бывает).

Определенный выше вектор действий игроков называется максиминным, или гарантирующим равновесием. Это один из вариантов определения исхода игры. То есть, можно предполагать, что возможный вариант поведения игроков - выбор всеми гарантирующих стратегий, что реализует максиминное равновесие.

Но этот вариант не единственен. И основная проблема теории игр на сегодняшний день заключается в том, что не существует единой универсальной концепции решения игры - ее устойчивого в том или ином смысле исхода. В разных моделях используются разные предположения, которые приводят к различным концепциям равновесия. Поэтому рассмотрим некоторые другие варианты.

2) Представим себе такую ситуацию, что целевая функция i -го игрока f_i (y) достигает максимума по его действию в точке, которая не зависит от действий других игроков. Это оптимальное действие, не зависящее от обстановки, называется доминантной стратегией агента. Формально: стратегия y_i^d будет доминантной стратегией, если какая бы обстановка не складывалась, его выигрыш будет максимальным при выборе именно доминантной стратегии:

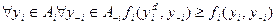
Отметим, что в обеих частях неравенства фигурирует произвольная, но одна и та же обстановка.

Если у каждого игрока существует доминантная стратегия, то совокупность доминантных стратегий называется равновесием в доминантных стратегиях (РДС) 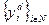. Это - идеальная ситуация для исследователя, описывающего математическую модель. Если существует равновесие в доминантных стратегиях, то каждый из игроков принимает решение независимо. А описывать независимое принятие решений гораздо проще. Но такая ситуация встречается очень редко.

3) Гораздо чаще существует равновесие Нэша (РН). Джон Нэш, американский математик, в начале 50-х годов XX века предложил следующее: устойчивым исходом взаимодействия агентов можно считать такой вектор их действий, от которого в одиночку никому не выгодно отклоняться. Это значит, что ни один из агентов, в одиночку меняя свою стратегию на другую, не может увеличить свой выигрыш при условии, что остальные своих стратегий не меняют.

Формальное определение равновесия Нэша 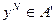таково: 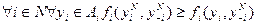, то есть для любого агента и для любого допустимого его действия выбор им равновесного по Нэшу действия дает ему выигрыш не меньший, чем при выборе любого другого действия при условии, что остальные игроки выбирают равновесные по Нэшу стратегии.

Пример 2.3. Рассмотрим двух агентов, представляющих подразделения некоторого предприятия. Каждый из агентов принимает решение о выборе неотрицательного объема производства. Продукция каждого из агентов продается на рынке по единичной цене. Затраты агента зависят от эффективности его производства (коэффициента r функции его затрат) и объема производства другого агента, причем чем выше объем производства оппонента, тем ниже затраты данного агента. Целевая функция i -го агента f_i (y) представляет собой разность между его доходом y_i и затратами 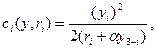i = 1, 2, где 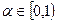– известная константа, отражающая степень взаимовлияния агентов.

Дифференцируя вогнутые по соответствующим переменным y_i целевые функции 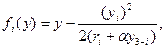i = 1, 2, приравнивая производные нулю и решая соответствующую систему уравнений относительно действий агентов, получаем равновесие Нэша игры агентов.

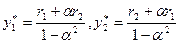Видно, что с ростом степени взаимовлияния агентов их равновесные действия увеличиваются.

Отличие между изложенными подходами заключается в том, что в определении равновесия в доминантных стратегиях фигурирует произвольная обстановка, то есть доминантная стратегия - наилучшая независимо от обстановки. А стратегия Нэша - наилучшая при «нэшевской» обстановке.

Равновесие Нэша хорошо тем, что в большинстве моделей оно существует. Недостатком его является то, что оно не всегда единственно. Представьте, если есть два равновесия, то как предсказать, в каком из них окажутся агенты? Нужны дополнительные предположения.

Кроме того, равновесие Нэша не устойчиво к отклонению двух и более игроков. По определению одному агенту не выгодно отклоняться, но это не значит, что если два агента договорились и одновременно отклонились, то они не смогут оба выиграть. То есть, равновесие Нэша - существенно некооперативная концепция равновесия.

4) Помимо вышесказанного, необходимо ввести понятие точки Парето. Вектор действий агентов 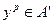, принадлежащий множеству A' допустимых векторов действий, будет эффективным по Парето, если для любого другого вектора действий найдется агент такой, что значение его целевой функции будет строго меньше, чем в точке Парето .

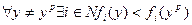То есть точка Парето - такая точка, отклоняясь от которой, нельзя одновременно увеличить значения целевых функций всех игроков. Идея хороша тем, что позволяет утверждать, что если мы можем сделать лучше всем, то это надо делать. Любая разумная модель должна удовлетворять эффективности по Парето. Вопрос заключается в том, как соотносятся все вышеперечисленные стратегии с эффективностью по Парето, так как хочется, чтобы результат, соответствующий индивидуальным максимумам, был бы еще эффективным для общества в целом. Оказывается, что эффективность по Парето, к сожалению, никак не соотносится ни с одной из трех концепций решения игры, изложенных выше.

Пример 2.4. Рассмотрим хрестоматийный пример со следующими целевыми функциями. Пусть каждый игрок выбирает действия из отрезка A_i =[0;1]. Выигрыш i -го агента - 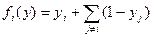. Исследуем, существует ли в рассматриваемом примере равновесие в доминантных стратегиях или равновесие Нэша.

Из анализа целевой функции видно, что i -му агенту выгодно, максимизируя свою целевую функцию, выбирать максимальное значение своего действия, независимо от того, какие действия выбирают остальные агенты (производная целевой функции i-го агента по его действию строго положительна независимо от обстановки). Значит, каждый агент будет выбирать максимальное значение своего действия, то есть для него существует доминантная стратегия. Что бы не сделали остальные, он, увеличивая свое действие, выигрывает, а больше единицы он (в силу ограниченности множества его допустимых действий) выбрать не может, значит, y_i^d= 1.

Посчитаем выигрыш каждого агента от равновесия в доминантных стратегиях. Если все выбрали по единице, то каждый получил выигрыш, равный единице: f_i (y^d)=1.

Рассчитаем вектор действий, эффективный по Парето. Это - вектор нулевых действий: y_i^P= 0. Если все агенты выбирают нулевые действия, выигрыш i -го агента равен f_i (y^P)= n- 1. Невозможно увеличить выигрыш одновременно всех агентов. Если мы хотим увеличить выигрыш i -го агента и начинаем увеличивать его действие, то тем самым уменьшаем выигрыши остальных, потому что это действие входит со знаком минус в целевые функции других агентов.

Если в рассматриваемой игре участвуют три или более агентов, то, выбирая действия, эффективные по Парето, они получают строго больше, чем выбирая доминантные стратегии, так как n- 1>1 при.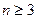

Спрашивается, будет ли точка Парето точкой равновесия Нэша (ведь любое РДС является равновесием Нэша), то есть рациональным исходом с точки зрения индивидуального поведения. Если кто-то из игроков выберет ненулевую стратегию, он выиграет. Поэтому он увеличит свое действие до единицы, остальные поступят анало­гично, и все скатится к ситуации равновесия в доминантных страте­гиях, которая никому не выгодна, но устойчива.

Рассмотренный пример иллюстрирует, что устойчивость относительно индивидуальных отклонений никак не связана с эффективностью по Парето. Решить эту проблему можно следующим образом: если разыгрывается повторяющаяся игра, и игроки договариваются наказывать того, кто отклоняется от коллективного оптимума, то есть от равновесия по Парето, то оказывается, если наказание достаточно сильно, то каждый будет выбирать индивидуально устойчиво ту стратегию, которая выгодна для всех.

Существует другой вариант, как можно достичь того же. Если агенты равноправны, то можно принять решение назначить им начальника, который будет ответственен за то, чтобы они не отклонялись, не пытались локально увеличить свой выигрыш, а выбирали равновесие, эффективное по Парето. То есть функция начальника - предотвратить отклонения агентов от оптимума по Парето. В случае трансферабельной полезности можно даже рассчитать, сколько агенты могут выделить на содержание такого начальника (как разность между тем суммарным выигрышем, который они имели в точке Парето, и тем, что они в сумме имеют при равновесии в доминантных стратегиях). Подобные рассуждения являются одним из теоретико-игровых обоснований возникновения иерархий.

Иерархические игры. С точки зрения управления наибольший интерес представляют модели игр, в которых агенты принимают решения не одновременно, а последовательно, то есть, если имеются управляющий орган и управляемые субъекты, то сначала начальник определяет правила игры, а дальше субъекты принимают решения, исходя из этих правил. Такие игры называются иерархическими. По определению, иерархическая игра – игра с фиксированной последовательностью ходов.

Простейшая модель иерархической игры – игра двух лиц, в которой первый (делающий первый ход) игрок – центр (управляющий орган), второй игрок – агент (см. рис. 2.1).

Пусть целевая функция центра Ф (u, y) зависит от выбираемого им действия 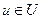и действия 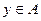агента, и целевая функция агента 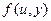зависит от тех же самых переменных. С одной стороны, если не введено условие последовательности выбора стратегий, то получается игра двух лиц в нормальной форме, тогда возможно достижение равновесия Нэша и т.п.

Предположим, что ситуация такова: центр выбрал своё действие и сообщил его агенту. Соответствующая игра называется игрой Г₁ и ее исследование состоит в следующем – описать, каким образом будет вести себя агент, зная выбор центра.

Найдем множество тех действий, на которых достигается максимум целевой функции агента при фиксированном выборе центра: 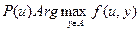. Понятно, что это множество зависит от того выбора 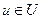, который сделал центр. Другими словами, действие центра может интерпретироваться как «управление», так как от него зависит «состояние» агента. Если центр и агент знают целевые функции и допустимые множества друг друга, то центр может предсказать, как отреагирует агент: «если агент рационален, то в ответ на мое действие, он выберет одно из действий из множества действий, доставляющих максимум его целевой функции». Как же следует вести себя центру, чтобы побудить агента выбрать действие, нужное центру? Зная свой выигрыш Ф (u, y), который зависит от своего действия и действия агента, центр должен определить, какое действие выберет агент из известного множества P (u).

Это множество может состоять из одной точки или из нескольких. Во втором случае следует ввести определенное предположение, как поведет себя агент. Типичных предположений два: критерии оптимизма и пессимизма (см. выше). Критерий оптимизма: агенту в принципе все равно (с точки зрения значений его целевой функции), какое действие из множества P (u) выбирать. Центр может рассуждать так: если агенту все равно, какое действие выбирать, будем считать, что он выберет действие, которое выгодно мне. Это предположение соответствует принципу оптимизма в теории принятия решений (см. выше). Называется оно гипотезой благожелательности. То есть агент настроен благожелательно к центру и выбирает из множества действий, которые максимизируют его целевую функцию, то действие, которое наиболее выгодно для центра.

Если вычислить максимум функции Ф (u, y) по действию агента, то останется зависимость только от действий центра. Центр, как рациональный игрок, будет выбирать такое свое действие, которое максимизирует его целевую функцию. Значит, оптимальным «управлением» (решением иерархической игры) будет действие центра, которое доставляет максимум по множеству допустимых управлений от его выигрыша Ф (u, y), в который подставлен максимум по множеству реакций агента:

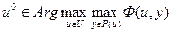
Пессимистический подход (принцип максимального гарантированного результата) – центр рассуждает так: агенту все равно, какое действие выбрать из множества P (u), поэтому я буду ориентироваться на наихудший случай. Тогда решение следующее:

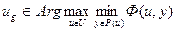
Т.е., центр вычисляет минимум своей целевой функции по действию агента из множества P(u), а дальше максимизирует выбором своего действия.

Таким образом, мы получаем два различных решения игры. Первое определение решения игры называется решением Штакельберга (немецкий экономист, в 30-х годах XX века разработавший рассматриваемую модель игры). Второе решение называется решением игры Г₁.

Рассмотрим теперь игру, когда центр сообщает агенту не конкретное значение управления, а то, каким будет управление в зависимости от действия агента.

Эта ситуация моделируется игрой Г₂, которая имеет следующий вид: выбор центра является функцией от действия агента 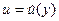. Дальнейшая логика рассуждений аналогична предыдущей: центр может предсказать, что в зависимости от той функции, которую он назначит, агент выберет действие, которое будет максимизировать его целевую функцию, в которую подставлен выбор центра: .

Зная это, центр может решать задачу, например, такую:

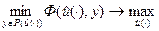
Данное выражение является стандартной записью простейшей теоретико-игровой задачи управления в организационной системе.

С содержательной точки зрения задача очень простая: есть два агента, известны их целевые функции, допустимые множества, нет никакой неопределенности.

С точки зрения математики: есть функционал, следует взять минимум этого функционала по переменной, которая принадлежит множеству, зависящему от искомой функции. Потом то, что получено, нужно максимизировать выбором этой функции.

Решение игры Г₂ было найдено советским ученым Ю.Б. Гермейером, который доказал, что в случае, когда возможны побочные платежи (аддитивно входящие в целевые функции игроков), оптимальная стратегия центра состоит из двух режимов: режима поощрения (агент поощряется за выбор требуемых центру действий) и режима наказания (агент наказывается центром при выборе действий, невыгодных для последнего). Этот результат широко используется при решении задач стимулирования в организационных системах (см. лекцию 4).

Кроме того, можно построить игру Г₃, в которой центр будет сообщать агенту зависимость управления от того, как в зависимости от управления будет вести себя агент. То есть стратегия агента становится функцией, а стратегия центра является функцией от этой функции (для сравнения: в игре Г₁ имеем два скаляра, в игре Г₂ – функцию и скаляр и т.д.).

Возможно построить игру Г₄, где стратегия центра будет функцией от функции от функции от функции. То есть с точки зрения математики усложнять структуру выбираемых участниками действий можно до бесконечности, и можно строить игры любого сколь угодно большого порядка, только проинтерпретировать их будет сложно.

У игры Г₃ простая интерпретация: начальник говорит подчиненному: «Я тебе выделяю ресурс, ты сообщи мне, как ты его будешь использовать в зависимости от того, сколько ресурса получишь. А в зависимости от этого, я буду его выделять».

У Г₄ интерпретация уже сложнее. Возникает вопрос: а дает ли что-нибудь начальнику вложенность игр (рост «уровня рефлексии»). Например, выгоднее ли ему Г₁₀₆, чем Г₁₀₁₅?

Н.С. Кукушкин доказал теорему, которая утверждает, что все четные игры вида Г_2k, где k = 1, 2, …, эквивалентны (с точки зрения выигрыша центра) игре Г₂. Все нечетные игры Г_2k+1 эквивалентны игре Г₃. То есть всю бесконечную совокупность иерархи­ческих игр порядка больше трех свели к двум играм – Г₂ и Г₃. Кроме этого, было доказано, что с точки зрения центра эффективность этих игр упорядочена следующим образом: _.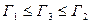

Вывод из теоремы Кукушкина следующий: если центр может, то ему надо разыгрывать игру Г₂, она для него наиболее выгодная и наиболее простая. Если не может, то игру Г ₃, если не может разыграть и ее, то – Г ₁. Играть же игры порядка 4 и выше не имеет смысла никогда!

Игры и структуры. Логичным продолжением перехода от игр в нормальной форме к иерархическим играм может быть следующее рассуждение: можно усложнять структуру дальше, но на самом деле существует единая технология описания теоретико-игровых задач управления в различных структурах.

Рассмотрим основную идею, которая позволяет видеть картину целиком и следить за логикой перехода от более простых к более сложным задачам, чтобы более сложная задача могла быть декомпозирована на более простые, и не казалась чем-то необычным.

Рассмотрим следующую картинку – см. рис. 2.2. Одного субъекта (рис. 2.2а) мы описывали с точки зрения гипотезы рационального поведения (ГРП), то есть агент стремится максимизировать свою функцию полезности, выбирая действие, которое доставляет максимум этой функции. Далее мы усложнили ситуацию и рассмотрели несколько субъектов на одном уровне (рис. 2.2б). Описали это взаимодействие игрой Г ₀ в нормальной форме. Затем была рассмотрена ситуация с двумя агентами, но взаимодействующими по вертикали (рис. 2.2в). Описывается их взаимодействие игрой Г_i, где i =1, 2, 3.

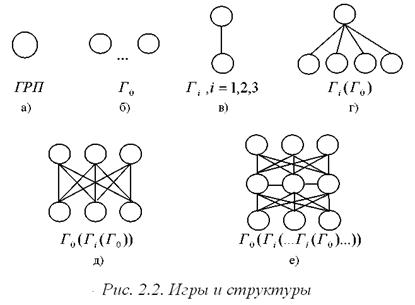
Представим себе, что имеется структура «один начальник – несколько подчиненных» (рис. 2.2г). Как ее можно описать? Взаимодействие агентов, находящихся на одном уровне, можно описывать игрой Г ₀. Взаимодействие «начальник-подчиненный» описывается игрой Г_i. Тогда условно такую структуру можно представить игрой Г_i, определенной «на игре» Г ₀. То есть это – иерархическая игра, но уже не на одном субъекте, который максимизирует свою целевую функцию, а на наборе субъектов, разыгрывающих свою игру.

Далее пусть есть несколько начальников (центров) и несколько подчиненных – агентов (рис. 2.2д). В общем случае каждый связан с каждым. Как это можно отразить? На нижнем уровне агенты играют игру Г ₀. Над ними центры разыгрывают иерархическую игру Г_i, но центры в свою очередь разыгрывают на своем уровне игру Г ₀. Получим игру Г ₀(Г_i (Г ₀)).Такова конструкция: берется сложная структура и разбивается (декомпозируется) на более простые.

Можно взять более сложную структуру с более сложным взаимодействием (например, рис. 2.2е). Это будет иерархическая игра между уровнями, на горизонтальных уровнях – обычная игра и т.д. Качественно ничего не меняется, усложняется только формальная задача, идеология описания остается та же.