Распределенный контроль

Усложним задачу дальше. Решим задачу управления для структуры, приведенной на рис. 4.12. Такие структуры называются системами с распределенным контролем. Это - перевернутая веерная структура, в которой один агент подчинен нескольким начальникам.

Ситуация достаточно распространена, в частности, в проектном управлении: агент, который работает по какому-то проекту, подчинен руководителю проекта; в то же время, он работает в подразделении и подчинен соответствующему функциональному руководите­лю. Или преподаватель работает на кафедре, а его приглашают читать лекции на другую кафедру или факультет.

Система с распределенным контролем характеризуется тем, что, если в веерной структуре имела место игра агентов, то в этой структуре имеет место игра центров. Если добавить сюда еще нескольких агентов, каждый из которых подчинен разным центрам, то получится игра и тех, и других на каждом уровне (см. рис. 2.2д). Опишем модель, которая сложнее рассмотренной выше многоэлементной системы, так как, если игра агентов заключается в выборе действий, а действием был скаляр, то игра центров заключается в выборе функций стимулирования агента, зависящих от его действий, то есть в игре центров стратегией каждой из них является выбор функции. Целевые функции центров имеет следующий вид:

;

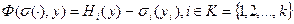и представляют собой разность между доходом и стимулированием, выплачиваемым агенту, где К- множество центров.

Целевая функция агента: 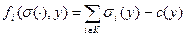, то есть он получает стимулирования от центров, которые суммируются, и несет затраты.

Предположим, что действия агента принадлежат множеству, которое будет уже не отрезком действительной оси (часы, шт. и т.д.), а может быть многомерным множеством (отражать разные виды деятельности), тогда функция затрат будет отображать множество действий во множество действительных чисел.

Определим множество выбора агента - множество максимумов его целевой функции в зависимости от стимулирования со стороны

центров: .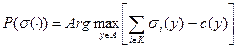

Поведение агента понятно: в зависимости от вектора стимулирований агент будет выбирать действие, которое будет максимизировать его целевую функцию, представляющую собой разность между его суммарным вознаграждением и затратами.

Тогда центры должны решить, какое стимулирование назначать агенту. Причем, каждый должен решить сам, как ему управлять подчиненным, что ему обещать. Центры оказываются «завязанными» на одного подчиненного, и что он будет делать, зависит от того, что ему предложит каждый из центров.

Каждый из центров не может рассуждать по отдельности, то есть, если он попросит от агента что-то сделать, то тот не обязательно это сделает, так как другой центр может попросить от него другого и пообещает заплатить больше. Таким образом, центры вовлечены в игру и должны прийти к равновесию, подбирая соответствующие функции стимулирования и прогнозируя, какие действия в ответ на вектор стимулирований будет выбирать агент.

Задача достаточно громоздка, поэтому приведем несколько известных результатов, которые позволяют ее упростить.

Первый результат говорит следующее: если рассматривается игра центров, то в теории игр принято использовать два подхода: равновесие Нэша и эффективность по Парето. В системе с распределенным контролем множество равновесий Нэша пересекается с множеством Парето, то есть можно из множества равновесий Нэша выбрать такое, которое является эффективным по Парето. Есть теорема, которая гласит, что существует класс простых функций стимулирования, которые гарантируют Парето-эффективность равновесия Нэша игры центров. Эти функции стимулирования имеют компенсаторный вид: , .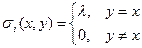

Содержательно эта система стимулирования значит, что существует некоторое действие агента (план x), относительно которого центры договорились выплачивать агенту стимулирование в случае, если он выберет это действие. При этом i -ый центр платит за выполнение плана. В случае, если агент выполняет другое действие, то он не получает вознаграждения вовсе. Таким образом, этот результат позволяет нам перейти от игры центров, в которой стратегией каждого является выбор функции, к игре, в которой стратегией является выбор одного действия агента и размера вознаграждения. Причем, относительно вектора вознаграждений можно сказать следующее: посмотрим на целевую функцию агента: он получает сумму вознаграждений и несет какие-то затраты. Если затраты в нуле равны нулю, то с точки зрения агента сумма стимулирований должна быть не меньше, чем затраты: .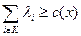

С другой стороны, Парето-эффективными с точки зрения центров являются такие размеры вознаграждений, которые нельзя уменьшить, не изменив действия агента. Значит, сумма вознаграждений должна быть в точности равна затратам агента.

Пользуясь этим результатом, охарактеризуем равновесие игры центров, то есть найдем такие условия, при которых они договорятся, чего хотят добиться от агента. Для этого рассчитаем следующие величины: .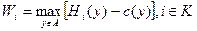

Если i -ый центр сам взаимодействует (работает в одиночку) с агентом, то он будет использовать компенсаторную систему стимулирования, и прибыль, которую он получит, будет равна величине W_i (это следует из решения одноэлементной задачи - см. выше).

Запишем условия того, что каждому центру будет выгодно взаимодействовать с другими центрами (совместно управлять агентом), по сравнению с индивидуалистическим поведением, когда он говорит: пусть подчиненный работает только на меня. Запишем это условие следующим образом: 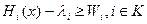. В случае если центры взаимодействуют друг с другом, i -ый центр получает доход H_i (x) от выбора агентом действия x и платит агенту . При этом значение его целевой функции должно быть не меньше, чем если бы он взаимодействовал с агентом в одиночку, что дало бы ему полезность W_i. Кроме того, должно быть выполнено условие равенства суммы вознаграждений агента его затратам. Обозначим:

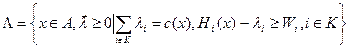- множество действий агента и векторов выплат его деятельности со стороны центров, таких, что сумма этих выплат в точности равна затратам агента по реализации этого действия, и каждый из центров получает выигрыш, не меньший, чем если бы он действовал в одиночку. Эта область представляет собой подмножество декартова произведения множества A на k -мерный положительный ортант.

Множество есть множество компромисса для системы с распределенным контролем. Она содержательно похожа на область компромисса в игре одного центра и одного агента.