Рассмотрим двухуровневую многоэлементную ОС, состоящую из центра и n агентов. Стратегией каждого из агентов является сообщение центру некоторой информации 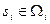 ,
, 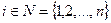 . Центр на основании сообщенной ему информации назначает агентам планы
. Центр на основании сообщенной ему информации назначает агентам планы 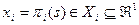 , где
, где 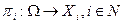 , - процедура (механизм) планирования,
, - процедура (механизм) планирования, 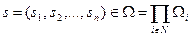 - вектор сообщений всех агентов.
- вектор сообщений всех агентов.
Функция предпочтения агента, отражающая интересы агента в задачах планирования: 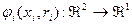 ,зависит от соответствующей компоненты назначенного центром плана и некоторого параметра - типа агента. Под типом агента обычно понимается точка максимума его функции предпочтения, то есть наиболее выгодное с его точки зрения значение плана.
,зависит от соответствующей компоненты назначенного центром плана и некоторого параметра - типа агента. Под типом агента обычно понимается точка максимума его функции предпочтения, то есть наиболее выгодное с его точки зрения значение плана.
На момент принятия решений каждому агенту известны: процедура планирования, значение его собственного типа 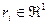 (идеальной точки, точки пика), целевые функции и допустимые множества всех агентов. Центру известны зависимости
(идеальной точки, точки пика), целевые функции и допустимые множества всех агентов. Центру известны зависимости 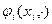 и множества возможных сообщений агентов и неизвестны точные значения типов агентов. Последовательность функционирования следующая: центр выбирает процедуру планирования и сообщает ее агентам, агенты при известной процедуре планирования сообщают центру информацию, на основании которой и формируются планы.
и множества возможных сообщений агентов и неизвестны точные значения типов агентов. Последовательность функционирования следующая: центр выбирает процедуру планирования и сообщает ее агентам, агенты при известной процедуре планирования сообщают центру информацию, на основании которой и формируются планы.
Так как решение, принимаемое центром (назначаемые агентам планы), зависит от сообщаемой агентами информации, последние могут воспользоваться возможностью своего влияния на эти решения, сообщая такую информацию, чтобы получить наиболее выгодные для себя планы. Понятно, что при этом полученная центром информация в общем случае может не быть истинной. Следовательно, возникает проблема манипулирования.
Как правило, при исследовании механизмов планирования, то есть в ОС с сообщением информации, вводится предположение, что функции предпочтения агентов однопиковые с точками пика 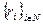 , то есть функция предпочтения
, то есть функция предпочтения 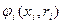 непрерывна, строго монотонно возрастает до единственной точки максимума ri и строго монотонно убывает после нее. Это предположение означает, что предпочтения агента на множестве допустимых планов таковы, что существует единственное наилучшее для него значение плана - точка пика, степень же предпочтительности остальных планов монотонно убывает по мере удаления от идеальной точки - точки пика.
непрерывна, строго монотонно возрастает до единственной точки максимума ri и строго монотонно убывает после нее. Это предположение означает, что предпочтения агента на множестве допустимых планов таковы, что существует единственное наилучшее для него значение плана - точка пика, степень же предпочтительности остальных планов монотонно убывает по мере удаления от идеальной точки - точки пика.
Будем считать, что агенты ведут себя некооперативно, выбирая доминантные или равновесные по Нэшу стратегии. Пусть 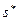 - вектор равновесных стратегий, если равновесий несколько, то необходимо ввести соответствие отбора равновесий, позволяющее из любого множества равновесий выбрать единственное. Очевидно, точка равновесия
- вектор равновесных стратегий, если равновесий несколько, то необходимо ввести соответствие отбора равновесий, позволяющее из любого множества равновесий выбрать единственное. Очевидно, точка равновесия 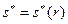 в общем случае зависит от вектора r= (r 1, r 2, …, rn) типов всех агентов.
в общем случае зависит от вектора r= (r 1, r 2, …, rn) типов всех агентов.
Соответствующим механизму 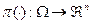 прямым механизмом планирования
прямым механизмом планирования 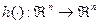 называется механизм
называется механизм 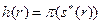 , ставящий в соответствие вектору точек пика агентов вектор планов. Термин «прямой» обусловлен тем, что агенты сообщают непосредственно (прямо) свои точки пика (в исходном - непрямом - механизме
, ставящий в соответствие вектору точек пика агентов вектор планов. Термин «прямой» обусловлен тем, что агенты сообщают непосредственно (прямо) свои точки пика (в исходном - непрямом - механизме 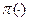 они могли сообщать косвенную информацию). Если в соответствующем прямом механизме сообщение достоверной информации является равновесной стратегией всех агентов, то такой механизм называется эквивалентным прямым (неманипулируемым) механизмом.
они могли сообщать косвенную информацию). Если в соответствующем прямом механизме сообщение достоверной информации является равновесной стратегией всех агентов, то такой механизм называется эквивалентным прямым (неманипулируемым) механизмом.
Рассмотрим возможные способы обеспечения достоверности сообщаемой информации. Наиболее очевидной является идея введения системы штрафов за искажение информации (в предположении, что центру в конце концов становятся известными истинные значения параметров 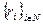 . Введением «достаточно сильных» штрафов действительно можно обеспечить достоверность сообщаемых оценок. Если отказаться от предположения, что центру становятся известными
. Введением «достаточно сильных» штрафов действительно можно обеспечить достоверность сообщаемых оценок. Если отказаться от предположения, что центру становятся известными 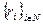 , то возникает задача идентификации неизвестных параметров по имеющейся у центра информации и, следовательно, задача построения системы штрафов за косвенные показатели искажения информации.
, то возникает задача идентификации неизвестных параметров по имеющейся у центра информации и, следовательно, задача построения системы штрафов за косвенные показатели искажения информации.
Другим возможным способом обеспечения достоверности сообщаемой информации является использование прогрессивных механизмов, то есть таких механизмов, в которых функция 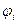 , при любой обстановке монотонна по оценке
, при любой обстановке монотонна по оценке 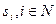 . Понятно, что если при этом справедлива «гипотеза реальных оценок»:
. Понятно, что если при этом справедлива «гипотеза реальных оценок»: 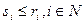 , то доминантной стратегией каждого агента будет сообщение
, то доминантной стратегией каждого агента будет сообщение 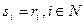 .
.
Условие совершенного согласования. Принцип открытого управления. Фундаментальным результатом теории активных систем является принцип открытого управления (ОУ). Основная его идея заключается в том, чтобы использовать процедуру планирования, максимизирующую целевую функцию каждого агента, в предположении, что сообщаемая агентами оценка достоверна. То есть центр идет навстречу агентам, рассчитывая на то, что и они его не «обманут». Это объясняет другое название механизма открытого управления - «механизм честной игры». Дадим строгое определение.
Условие:
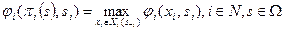 ,
,
где Xi(s-i) - децентрализующее множество - устанавливаемое центром множество планов, зависящее от обстановки s-i=(s 1, s2, …, si-1, si+ 1, …, sn) для i- го агента, 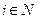 , называется условием совершенного согласования.
, называется условием совершенного согласования.
Процедура планирования, максимизирующая целевую функцию центра 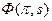 на множестве планов, удовлетворяющих условиям совершенного согласования, называется законом открытого управления.
на множестве планов, удовлетворяющих условиям совершенного согласования, называется законом открытого управления.
Имеет место следующий факт: для того чтобы сообщение достоверной информации было доминантной стратегией агентов, необходимо и достаточно, чтобы механизм планирования был механизмом открытого управления.
Приведенное утверждение не гарантирует единственности ситуации равновесия. Конечно, если выполнено условие благожелательности (если 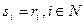 - доминантная стратегия, то агенты будут сообщать достоверную информацию), то использование закона ОУ гарантирует достоверность сообщаемой агентами информации.
- доминантная стратегия, то агенты будут сообщать достоверную информацию), то использование закона ОУ гарантирует достоверность сообщаемой агентами информации.
Приведем достаточное условие существования единственной ситуации равновесия вида 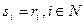 ,в системе с законом ОУ. Обозначим:
,в системе с законом ОУ. Обозначим: 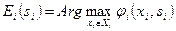 - множество согласованных планов i -го агента. Будем считать, что для i -го агента выполнено условие равноправия функций предпочтения, если имеет место:
- множество согласованных планов i -го агента. Будем считать, что для i -го агента выполнено условие равноправия функций предпочтения, если имеет место:
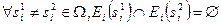 ,
,
то есть при любых допустимых несовпадающих оценках 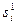 и
и 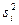 соответствующие множества согласованных планов не пересекаются. Справедливо следующее утверждение: условие равноправия функций предпочтения для всех агентов является достаточным условием единственности ситуации равновесия.
соответствующие множества согласованных планов не пересекаются. Справедливо следующее утверждение: условие равноправия функций предпочтения для всех агентов является достаточным условием единственности ситуации равновесия.
Необходимым и достаточным условием сообщения достоверной информации как доминантной стратегии при любых идеальных точках 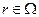 является существование множеств
является существование множеств 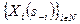 для которых выполнены условия совершенного согласования. Данное утверждение можно переформулировать следующим образом: если в исходном механизме планирования существует равновесие в доминантных стратегиях, то соответствующий прямой механизм будет неманипулируем.
для которых выполнены условия совершенного согласования. Данное утверждение можно переформулировать следующим образом: если в исходном механизме планирования существует равновесие в доминантных стратегиях, то соответствующий прямой механизм будет неманипулируем.
Интересным и перспективным представляется геометрический подход к получению достаточных условий неманипулируемости путем анализа конфигураций множеств диктаторства (диктаторами называют агентов, получающих абсолютно оптимальные для себя планы), определяемых как множества таких значений типов агентов, что определенные агенты получают планы, строго меньшие оптимальных для них планов, равные оптимальным и строго бόльшие. В рамках этого подхода уже удалось получить ряд конструктивных условий индивидуальной и коалиционной неманипулируемости механизмов планирования в ОС.
Оптимальность механизмов открытого управления в организационных системах с одним агентом. До сих пор мы интересовались в основном условиями сообщения достоверной информации. Возникает закономерный вопрос: как соотносятся такие свойства механизма функционирования, как неманипулируемость и оптимальность? Иначе говоря, всегда ли среди оптимальных механизмов найдется неманипулируемый и, соответственно, всегда ли среди неманипулируемых механизмов содержится хоть один оптимальный. Получить ответ на этот вопрос необходимо, так как, быть может, не обязательно стремиться к обеспечению достоверности информации, лишь бы механизм имел максимальную эффективность. Поэтому приведем ряд результатов по оптимальности (в смысле максимальной эффективности) механизмов открытого управления.
Известно, что в ОС с одним агентом для любого механизма существует механизм открытого управления не меньшей эффективности. Качественно этот факт объясняется тем, что для единственного агента децентрализующим множеством будет все множество его допустимых планов (другими словами, у одного агента всегда есть «доминантная» стратегия).
Для систем с бόльшим числом 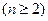 агентов вывод об оптимальности механизмов открытого управления справедлив лишь для ряда частных случаев. Например, аналогичные результаты были получены для механизмов распределения ресурса, для механизмов выработки коллективных экспертных решений (задач активной экспертизы) и механизмов внутренних цен, рассматриваемых в настоящей лекции ниже, а также для ряда других механизмов планирования.
агентов вывод об оптимальности механизмов открытого управления справедлив лишь для ряда частных случаев. Например, аналогичные результаты были получены для механизмов распределения ресурса, для механизмов выработки коллективных экспертных решений (задач активной экспертизы) и механизмов внутренних цен, рассматриваемых в настоящей лекции ниже, а также для ряда других механизмов планирования.
Полученные в теории активных систем результаты о связи оптимальности и неманипулируемости механизмов вселяют некоторый оптимизм, в том смысле, что эти два свойства не являются взаимно исключающими. В то же время, ряд примеров свидетельствуют о неоптимальности в общем случае механизмов, обеспечивающих сообщение агентами достоверной информации. Вопрос о соотношении оптимальности и неманипулируемости в общем случае остается открытым.
Выше при рассмотрении механизмов стимулирования в ОС согласованными были названы механизмы, побуждающие агентов к выполнению планов. В ОС, в которых стратегией агентов является выбор как сообщений, так и действий (комбинация задач стимулирования и планирования), механизмы, являющиеся одновременно согласованными и неманипулируемыми, получили название правильных. Значительный интерес представляет вопрос о том, в каких случаях оптимальный механизм можно искать в классе правильных механизмов.
Гипотеза слабого влияния. Пусть часть плановых показателей 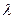 в системе с большим числом агентов является общей для всех агентов, то есть номенклатура плана имеет вид:
в системе с большим числом агентов является общей для всех агентов, то есть номенклатура плана имеет вид: 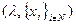 . Если искать управления
. Если искать управления 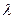 , выгодные для всех агентов (как это делается при использовании принципа согласованного планирования), то возникает принципиальный вопрос о существовании решения.
, выгодные для всех агентов (как это делается при использовании принципа согласованного планирования), то возникает принципиальный вопрос о существовании решения.
Такого рода проблем не возникает в системах с большим числом агентов, когда влияние оценки отдельного агента на общее управление мало. Если при сообщении своей оценки si каждый агент не учитывает ее влияния на 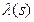 , то считается выполненной гипотеза слабого влияния (ГСВ). При справедливости ГСВ необходимо согласовывать планы только по индивидуальным переменным. Доказано, что если выполнена ГСВ и компоненты x (s) плана удовлетворяют условиям совершенного согласования, то сообщение достоверной информации является доминантной стратегией.
, то считается выполненной гипотеза слабого влияния (ГСВ). При справедливости ГСВ необходимо согласовывать планы только по индивидуальным переменным. Доказано, что если выполнена ГСВ и компоненты x (s) плана удовлетворяют условиям совершенного согласования, то сообщение достоверной информации является доминантной стратегией.
Перейдем к рассмотрению ставших уже хрестоматийными механизмов планирования в многоэлементных ОС, для которых оптимален принцип открытого управления.
 2014-02-02
2014-02-02 1205
1205
