Рассмотрим целевую функцию центра. Она представляет собой при использовании компенсаторной системы стимулирования с 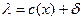 доход центра минус стимулирование агента:
доход центра минус стимулирование агента: 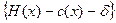 . Если вознаграждение агента равно затратам, то выигрыш центра в зависимости от того, какое действие он побуждает выбирать агента, представляет собой разность между доходом центра и затратами. Следовательно, нужно выбрать x *, который будет доставлять максимум по
. Если вознаграждение агента равно затратам, то выигрыш центра в зависимости от того, какое действие он побуждает выбирать агента, представляет собой разность между доходом центра и затратами. Следовательно, нужно выбрать x *, который будет доставлять максимум по 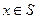 разности
разности 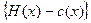 .
.
Таким образом, сначала имелась сложная система стимулирования – ее упростили до системы с двумя параметрами. Первый параметр рассчитали. Осталось найти второй параметр – план x*. Он должен быть такой, чтобы максимизировать разность между доходом центра и системой стимулирования, равной в точности затратам агента. В результате оптимальным решением задачи стимулирования будет компенсаторная система стимулирования такого вида, в которой размер вознаграждения равен затратам агента, а оптимальный план равен плану, максимизирующему разность между доходом центра и затратами агента. Окончательно оптимальное решение будет выглядеть следующим образом:
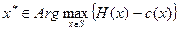 .
.
Рассмотрим данное решение задачи поиска оптимального плана x*. Это выражение означает, что разность между доходом центра и затратами агента – «толщина» области компромисса (см. рис. 4.3) – максимальна. При дифференцировании в точке x* угол наклона касательной к функции дохода центра будет равен углу наклона касательной к функции затрат агента. В экономике это интерпретируется как точка оптимума, в которой предельная производительность равна предельным затратам.
Значит, точка x * является оптимальной с точки зрения центра и реализуется исход, определяемый точкой В на рис. 4.3. Возможна другая ситуация. Рассмотрим модель, в которой первое предложение делает агент. Он предлагает центру: «я буду делать столько-то, а ты мне будешь платить столько-то». Если центр это устраивает, он соглашается.
Вопрос: что должен предложить агент? Агент должен предложить центру то же самое действие x*, а плату запросить соответствующую точке А на рис. 4.3. В этой ситуации всю «прибыль» [ H (x*) –c (x*)] будет забирать агент.
Другими словами, в данной игре выигрывает тот, кто делает ход первым. Если начальник, то он «сажает на ноль» подчиненного, если подчиненный, то он «сажает на ноль» начальника. В рамках формальной модели и тот, и другой на это согласятся.
Рассмотрим следующую ситуацию. Пусть заданы целевые функции центра и агента, в которых фигурируют доход центра и затраты агента. Переменная – функция стимулирования – является внутренней характеристикой системы, отражающей взаимодействие между центром и агентом: сколько центр отдал, столько агент и получил. Если просуммировать целевые функции центра и агента, то сократятся значения функции стимулирования, и останется разность доходов и затрат. Значит действие x*, которое является решением задачи стимулирования, максимизирует сумму целевых функций, то есть, действие агента, которое реализует центр, оптимально по Парето.
Можно ставить задачи определения конкретной точки внутри отрезка АБ на рис. 4.3. Мы рассмотрели две крайности:
1) всю прибыль себе забирает центр;
2) всю прибыль забирает агент.
Возможно определение компромисса между ними, то есть центр и агент могут договориться делить эту прибыль, например, пополам. Тогда агент, кроме компенсации затрат, получает половину этой прибыли. Или другой принцип: фиксированный норматив рентабельности, то есть пусть стимулирование агента составляет не только затраты, а затраты, умноженные на единицу плюс норматив рентабельности. Аналогично анализируется большое количество модификаций задачи стимулирования.
Решение задачи найдено – компенсаторная система стимулирования с планом x*. Единственно ли оно? Рассуждение очень простое: пусть есть функция затрат агента, и есть план x *. Оптимальная система стимулирования – квазикомпенсаторная – побуждает агента выбирать x *, и центр несет затраты на стимулирование в точности равные затратам агента.
Возьмем другие системы стимулирования, которые побуждают агента выбирать то же действие, а центр платить столько же. Для того чтобы такая система стимулирования существовала необходимо, чтобы функция стимулирования проходила через точку (x *, c (x *)).
Утверждение 4.2. Для того чтобы агент выбирал действие x*, достаточно, чтобы функция стимулирования проходила через точку (x*, c (x*)), а во всех остальных точках была не больше, чем затраты агента.
Если взять любую систему стимулирования из изображенных на рис. 4.11, то она тоже будет побуждать агента выбирать это действие, и центр будет платить столько же.
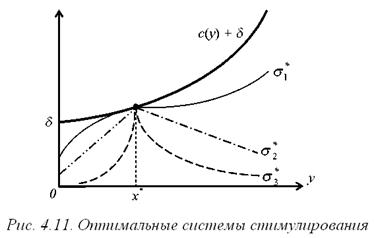
Можно взять скачкообразную систему стимулирования – при действиях, меньших плана, вознаграждение равно нулю, выполнил план – получил вознаграждение не меньшее затрат (аккордная оплата). Можно выбрать монотонную систему стимулирования, которая проходит через точку (x*, c (x*)), и всюду лежит ниже затрат. То есть любая кривая, проходящая через точку (x*, c (x*)) и лежащая ниже функции затрат, будет решением задачи стимулирования.
В табл. 4.1 приведены оценки сравнительной эффективности различных базовых систем стимулирования.
Табл. 4.1. Оценки сравнительной эффективности базовых системстимулирования
| K | C | L | LK | D | L+C | LL | |
| K | = | = | 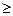 | = | 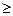 | = | = |
| C | = | = | 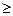 | = | 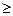 | = | = |
| L | 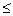 | 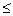 | = | 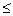 | ? | 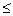 | 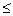 |
| LK | = | = | 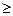 | = | 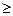 | = | = |
| D | 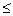 | 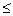 | ? | 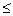 | = | 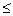 | 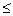 |
| L+C | = | = | 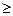 | = | 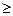 | = | = |
| LL | = | = | 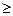 | = | 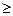 | = | = |
В данной таблице сравнительная эффективность семи базовых систем стимулирования (в предположении выпуклости и монотонности функции затрат агента), отражена следующим образом: если в ячейке стоит символ «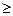 », то эффективность системы стимулирования, соответствующей строке, не ниже эффективности системы стимулирования, соответствующей столбцу (аналогичный смысл имеют и другие неравенства; символ «?» означает, что сравнительная эффективность систем стимулирования L-типа и D-типа в каждом конкретном случае зависит от функции затрат агента и функции дохода центра).
», то эффективность системы стимулирования, соответствующей строке, не ниже эффективности системы стимулирования, соответствующей столбцу (аналогичный смысл имеют и другие неравенства; символ «?» означает, что сравнительная эффективность систем стимулирования L-типа и D-типа в каждом конкретном случае зависит от функции затрат агента и функции дохода центра).
Параметрическое представление целевых функций. До сих пор мы рассматривали задачи, в которых ограничения на класс целевых функций агентов (точнее – на функции стимулирования) отсутствовали. На практике нередко класс целевых функций агентов задан в параметрическом виде f (x, y), где 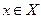 , X – множество значений параметра x. Представим f (x, y) в виде
, X – множество значений параметра x. Представим f (x, y) в виде
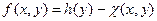
где h (y)= f (y, y), 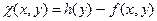 .
.
Параметр x естественно интерпретировать как плановое задание для агента (желательное для центра состояние агента), а 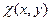 – как штраф при отклонении состояния от плана
– как штраф при отклонении состояния от плана 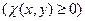 ,
, 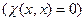 . В этом случае задача стимулирования фактически становится задачей планирования в условиях полной информированности. Задача оптимального планирования становится игрой Г 1 (см. лекцию 2). Определение решения этой игры называется принципом оптимального планирования с прогнозом состояния. Множество
. В этом случае задача стимулирования фактически становится задачей планирования в условиях полной информированности. Задача оптимального планирования становится игрой Г 1 (см. лекцию 2). Определение решения этой игры называется принципом оптимального планирования с прогнозом состояния. Множество
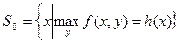
называется множеством согласованных планов, а определение оптимального плана на множестве согласованных планов называется принципом оптимального согласованного планирования.
Возникает вопрос, в каких случаях принцип оптимального планирования с прогнозом состояний эквивалентен принципу оптимального согласованного планирования (в каких случаях оптимальный план будет выполнен). Наиболее известным и изящным достаточным условием согласованности является так называемое «неравенство треугольника» для функции штрафов:
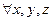
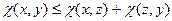 .
.
 2014-02-02
2014-02-02 890
890








